首先,有y = AX,将A看作是对X的线性变换
但是,如果有AX = λX,也就是,A对X的线性变换,就是令X的长度为原来的λ倍数。
*说起线性变换,A肯定要是方阵,而且各列线性无关。(回想一下,A各列相当于各个坐标轴,X各个分量相当于各个坐标轴的“基本向量”长度)
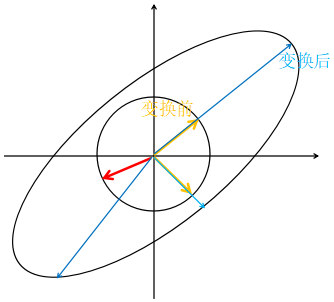 (同一长度的各个方向的向量,变换前和变换后,有些前后只是拉伸了,方向不变;有些拉伸了,方向同时也改变了)
(同一长度的各个方向的向量,变换前和变换后,有些前后只是拉伸了,方向不变;有些拉伸了,方向同时也改变了)
这样的X1,X2……Xn称为特征向量, λ1, λ2…… λn为对应的特征值。
如果有S矩阵,全是特征特征向量,也就是 S = [X1,X2……Xn]
![]()
AS=S∧,A = S∧ S-1 ,又叫矩阵对角化。(这是继LU分解,QR分解后的第三种分解)
(A = x1λ1 y1 + …… + xnλn yn , y1 ~ yn 假设是S-1 的行向量,如果λ1 是最大的,比其他大很多,那么对于A矩阵,只要记住x1λ1 y1 就可以有一个近似的A' ,实现了对矩阵的压缩存储)
*如果A能对角化,除了是方阵,还要各个λ值互不相同。因为λ有一对相同,证明X会有一对线性相关,从而S的列向量不独立,从而S没有逆。
既然这样,那么X可以单位化,也就是X' = X / ||X||,而 λ' = ||X|| λ , X重要的是方向,而不是长度。
如果A是对称矩阵,那么A = AT
A = S∧ S-1 = (S∧ S-1)T = (S-1) T ∧ST
要式子成立,那么S-1 = ST ,要有这种性质的矩阵S,只有标准正交矩阵Q,因为QQ-1 = I = QQT
对于A = AT ,有A = Q ∧QT , 并没有什么约束条件 (Gilbert Strang《Introduction to LINEAR ALGEBRA》p330),这就是对称矩阵对角化
(对称矩阵一定是方阵,但不一定有逆,如元素全是1的也对称,但各列向量不独立)
相似矩阵:如果M可逆,那么B = M-1AM相似于A,而且B的特征值和A的特征值一样。
证明:B = M-1AM 等价于 A = MBM-1 , AX =λX,(MBM-1)X=λX , B(M-1X) = λ(M-1X)。因此,B的特征向量是(M-1X) ,特征值依然是λ。
任意正交向量组V1,V2,V3,通过A变换(A可以是任意形式的矩阵),得到的向量都是正交的。
(这种任意m*n的变换,应该叫“仿射变换”,因为向量v变换后,其维数都不同了;而平时n*n的变换,应该叫线性变换,维数还是一样的)
证明:A是m*n的,v是n*1的,u是m*1的,那么:
Av1 = u1 ,
Av2 = u2
要证明U1TU2=0
(Av1) T(Av2 ) =u1Tu2 只要证明等式左边等于0
v1T AT Av2 = u1Tu2 因为ATA是对称矩阵,所以有:
v1T Q ∧QTv2 = u1Tu2
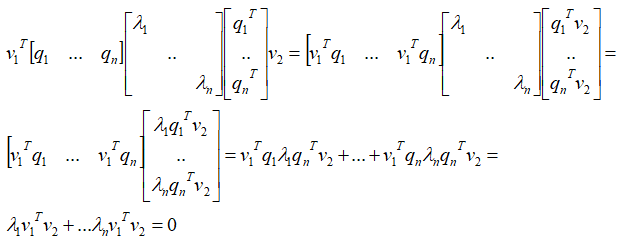
基于上面,假如将u单位化,v单位化,那么有:
Av1 = δ1u1 ,
Av2 = δ2u2
1. v的向量个数,顶多有n个,因为V为n维空间,n维空间中相互垂直的向量顶多有n个。
2. 就算v是长度为1,通过乘以矩阵A后,也有可能变为长度不为1的u,
假设所有n个相互正交的单位v向量,通过A变换后,得到相互正交的n个u向量, 将上式子写成矩阵形式:
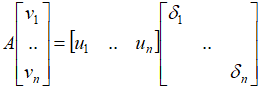
也就是:AV=UΣ
因为V是标准正交矩阵,所以VVT=I,所以:A=UΣVT 这就是著名的奇异值分解(SVD)
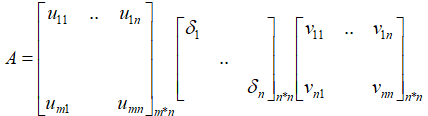
(奇异值分解,其实是通用的,终极的分解方式。一旦做SVD分解,自然会根据矩阵的特性,变为:1. 可逆且特征值不重复的方阵分解为S∧ S-1 ;2. 对称方阵分解为Q ∧QT ;3. 最一般的形式)
那么,现在的问题仅仅是,如何寻找V和U?
首先,我们已经知道,任意矩阵A,能分解为A=UΣVT , 所以,可以从这个入手:
(1)AAT =UΣVT VΣT UT
因为上式子中,V为单位正交矩阵,VTV = I,Σ为对角矩阵,ΣΣT = Σ2,所以有:
AAT = UΣ2 UT , 这不就是对称矩阵对角化 :U原来是AAT 的特征向量,Σ是AAT 的特征值开根号。
同理:
(2)ATA = VΣT UT UΣVT
ATA = VΣ 2VT ,那么:V原来是 ATA 的特征向量,Σ是AAT 或 ATA 的特征值开根号。
顺便有:
当m>n时:
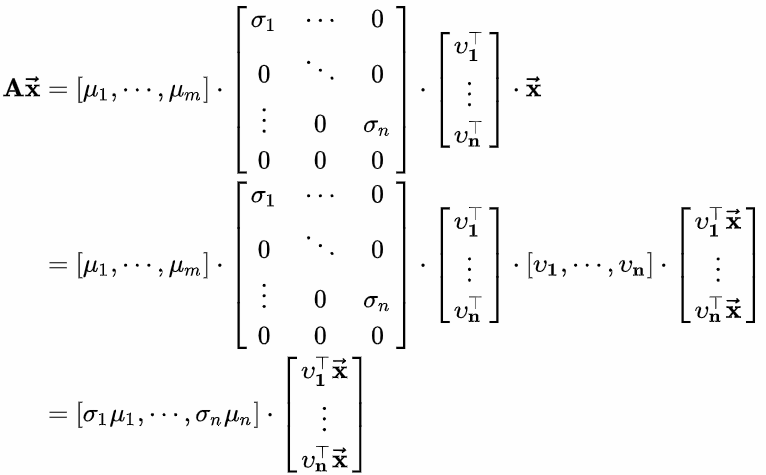
总结:计算的主要工作,是如何求解特征值的问题。这是《数值分析》的内容,在此不讲,只讲非数值分析的思路:
因为:AX =λX ,所以,(A-λI)X= 0
又因为X要有解,又不能全为0,所以A-λI 的各列要线性相关。
又因为A-λI 的各列要线性相关,所以行列式det(A-λI) = 0
(三维)行列式的几何意义是,三个向量作为边,形成的立体体积。
如果三个向量线性相关,那么自然被“压缩”到一个平面上,体积为0;
那么,只要用到 A-λI 的各列来求体积为0,就可以对λ列方程,就可以解λ。(实际上《数值分析》并不会这么解,是通过A*A*A*A....迭代得到的)
参考:
https://zhuanlan.zhihu.com/p/57803955 (推导过程)
https://zhuanlan.zhihu.com/p/42896542 (图片压缩和应用)