假设,问题是,要分析图像上一共有多少个正方形物体。
准备知识:
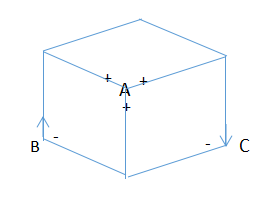
从屏幕视觉,看交点A、B、C,
+号代表凸线,往视觉方向延申;
箭头代表边界,箭头右侧代表图形内;
-号代表往视觉反方向延伸;
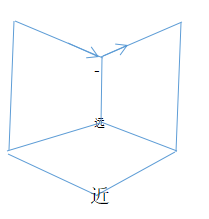
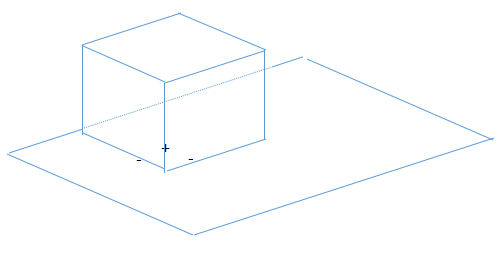
所以,对于不同的视角,不同的交点,一共有如下多种情况:

OK,假如有一个图像,检验其在真实世界中能不能构建,只要看看其各点,能不能由上述的情况组建:
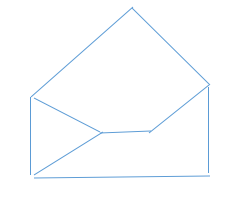
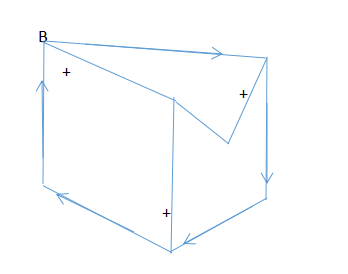
此图像是否能在真实世界中构建?
首先,能快速画边界线:
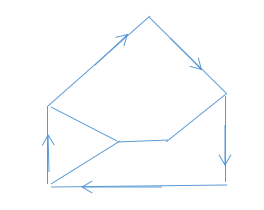
然后快速查表,中间可以用G或H代入,先用G代入:
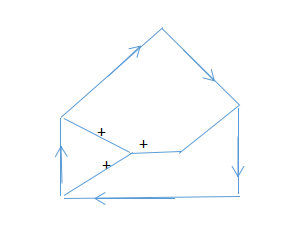
右侧用Q代入:
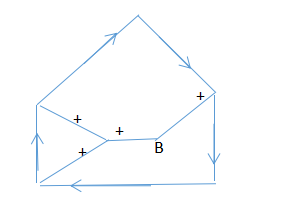
可以看出,B点已经不符合现实世界的规则了。
同理,使用其他组合,总有一个点,在上表中,找不到合适的规则,也就说明,这个图像不能构成3D图型;(不符合这个世界的可构性)
但是,即使每个点都能够找到与上表的规则,也不一定行,比如:
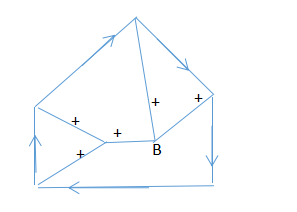
加上一条线之后,看似能构建,实际上也不行。
这个东西,按照规则是无法构造的,但是在现实世界中,显然是可以的;
这是因为,我们的问题立足点只是点最多连3个面,现实中很多点是连4个面,所以需要更多的规则。
那么,对于物体识别,通常又可以建立一颗“约束树”,有点像“博弈树”
1. 随机选一个节点开始,假如是B点,有Q、R、S三种构筑方法;
2. 对三种构筑方法,分别沿一条边线,寻找另一点A;假如另一点是“T”型,而且公共边线,既符合B点的选项,又有符合的“T”型构筑可选,那么可以对A的另一条边,继续寻找下一点;
.......
3. 对于沿着某条线,到了第n个点,可以从“视觉列表”中,找到各种“配型”。将那些边,和前面的边的性质有冲突的配型去除。
*对于每个扩展,都要记住每条边的性质,因为判别每个点的时候,要从“视觉列表”中找到的类型,要受到已经标记了的边的约束
*直到所有点,在约束内,都能从“视觉”列表找到匹配的,那一个形状的构筑就完成了。