1、模型描述
Univariate(One variable)Linear Regression
m=训练样本的数目,x's=输入的变量/特征,y's=输出变量/目标变量
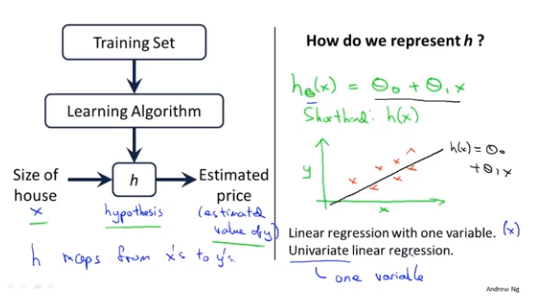
2、代价函数
基本定义:

3、代价函数(一)
回顾一下,前面一些定义:

简化的假设函数,theta0=0,得到假设函数与目标函数的关系有:
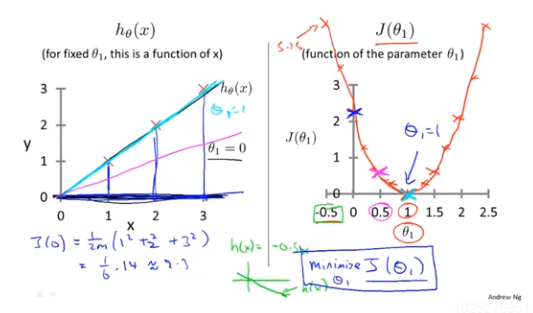
4、代价函数(二)
等高线图(contour figures):有相同的J(theta0,theta1)的值,对应着不同的theta0,theta1值。
下面介绍一种能自动得到使得目标函数最小的参数值的算法。。
5、梯度下降算法的梗概
特点:起始点不同,经过一次次的梯度下降,最后会到达不同的局部最优点。
算法:

上面第一行即updating equation(更新式)。
注意的几点:
- 当写成a:=b指的是将b的值赋给a(computer operation),而写成a=b时是判断操作(true assertion)
- alpha(learning rate)用来控制梯度下降的幅度/速度,如何设置它的值在之后会提到
- 导数项(后面推导)
- 保证参数的同步更新
6、梯度下降知识点总结
解释一下梯度下降算法的具体组成:
- learning rate始终是正数
- alpha过大或者过小都不好

- 参数已经处在局部最优点(导数为零),根据算法公式,参数不用更新
- 梯度下降的过程中,越来越接近局部最优处,导数值越来越小,梯度下降自动选择幅度较小的速率进行。。因故没有必要再另外减小alpha的值
7、线性回归的梯度下降
结合前面的,得到:

线性回归的代价函数是一个凸函数(形状上看似是一个弓状函数),只有一个全局最优点。
“Batch”梯度下降法:在每一步的梯度下降过程中都使用到了所有的训练数据。
在高等线性代数中有一种方法可以不需要使用梯度下降的迭代算法,可以直接求解出代价函数的最小值,即正规方程组方法(normal equation method)。
附上本章的ppt资料链接:https://study.163.com/course/courseLearn.htm?courseId=1004570029#/learn/text?lessonId=1050362429&courseId=1004570029