遗传算法中包含了如下5个基本要素:
(1)对参数进行编码;
(2)设定初始种群大小;
(3)适应度函数的设计;
(4)遗传操作设计;
(5)控制参数设定(包括种群大小、最大进化代数、交叉率、变异率等)。
下面使用python编程对中国28个省会城市的TSP问题进行了求解,python的版本是2.7.14。百度地图提供了JavaScript API,能够很方便地获取各城市之间的路径距离。这里有一段获取28个城市之间距离的JS代码,将其复制到百度地图JavaScript API的一些示例网页上,然后点击运行,再点击右侧相应的按钮即可获取各城市之间的距离。

1 <html> 2 <head> 3 <meta http-equiv="Content-Type" content="text/html; charset=utf-8" /> 4 <meta name="viewport" content="initial-scale=1.0, user-scalable=no" /> 5 <style type="text/css"> 6 body, html{ 100%;height: 100%;overflow: hidden;margin:0;font-family:"微软雅黑";} 7 #l-map{height:100px;100%;} 8 #r-result{100%; font-size:1px;line-height:12px;} 9 </style> 10 <script type="text/javascript" src="http://api.map.baidu.com/api?v=2.0&ak=您的密钥"></script> 11 <title>计算驾车时间与距离</title> 12 </head> 13 <body> 14 <div id="l-map"></div> 15 <div id="r-result"> 16 <input type="button" value = "计算各省会城市间距离矩阵" onclick = "getCityDistance()" /> 17 <div id="result"></div> 18 </div> 19 </body> 20 </html> 21 <script type="text/javascript"> 22 // 百度地图API功能 23 var map = new BMap.Map("l-map"); 24 map.centerAndZoom(new BMap.Point(116.404, 39.915), 5); 25 var city = [ 26 "北京", "长春", "沈阳", "哈尔滨", "石家庄", "济南", 27 "呼和浩特", "太原", "郑州", "南京", "上海", "杭州", 28 "福州", "南昌", "武汉", "合肥", "长沙", "广州", 29 "重庆", "西安", "海口", "贵阳", "昆明", "成都", 30 "兰州", "西宁", "拉萨", "乌鲁木齐" 31 ]; 32 33 var i = 0, j = 1; 34 35 function getCityDistance() 36 { 37 setInterval(getCityDistance1, 6000); 38 } 39 40 function getCityDistance1() 41 { 42 if(i >= city.length - 1) 43 { 44 return; 45 } 46 var output = ""; 47 city1 = city[i]; 48 city2 = city[j]; 49 var searchComplete = function (results) 50 { 51 if(transit.getStatus() != BMAP_STATUS_SUCCESS) 52 { 53 return ; 54 } 55 var plan = results.getPlan(0); 56 output += plan.getDistance(false) + ", "; //获取距离 57 document.getElementById("result").innerHTML += output; 58 } 59 var transit = new BMap.DrivingRoute( 60 map, 61 {renderOptions: {map: map, autoViewport: false}, onSearchComplete: searchComplete, onPolylinesSet: function(){}} 62 ); 63 64 transit.search(city1, city2); 65 66 j++; 67 if(j >= city.length) 68 { 69 i++; 70 j = i + 1; 71 } 72 73 } 74 </script>
第一步,初始化种群
# 创造生命集 for i in range(self.life_count): self.lives.append(Life(self.make_life())) # 创造新生命 def make_life(self): lst = range(self.gene_length) # 随机顺序 random.shuffle(lst) return lst
第二步,计算个体适应度
使用每个个体对应的路线总长度的倒数作为个体的适应度,也就是每个个体的得分
# 评价函数 def judge(self): self.bounds = 0.0 self.best = Life() self.best.setScore(-1.0) for lf in self.lives: lf.score = 1.0/self.distance(lf.gene) if lf.score > self.best.score: self.best = lf self.bounds += lf.score # 得到当前顺序下连线总长度 def distance(self, order): distance = 0 for i in range(-1, self.gene_length - 1): i1, i2 = order[i], order[i + 1] distance += self.get_city_distance(self.dist_matrix, self.gene_length, i1, i2) return distance
第三步,更新种群
(1)将种群中适应度最高(得分最高)的个体加入下一代种群中
(2)从种群中选择一些个体用于产生下一代,每个个体被选到的可能性与它的得分成正比。选择概率计算方式为

(3)从种群中选择两个个体后,以一定的概率进行交叉。交叉的方法为:从第二个个体基因的前段截取一段随机长度的基因接到第一个个体基因的前面,然后剔除其与截取基因段中重复的元素,最终得到一个新的基因
(4)以一定的概率对第(3)步得到的基因进行变异。变异的方法为:从基因中随机选取两个位置,将这两个位置的元素互换,并将其中一个元素转移到基因的末尾
(5)重复(2)到(4),直到产生的新个体数与原种群个体数相同为止
# 演化至下一代 def next(self): # 评估群体 self.judge() # 新生命集 newLives = [] # 将最好的父代加入竞争 newLives.append(Life(self.best.gene)) # 产生新的生命集个体 while(len(newLives) < self.life_count): newLives.append(self.bear()) # 更新新的生命集 self.lives = newLives self.generation += 1 # 产生后代 def bear(self): lf1 = self.get_onelife() lf2 = self.get_onelife() # 交叉 r = random.random() if r < self.overlapping_rate: gene = self.overlapping_func(lf1, lf2) else: gene = lf1.gene # 突变 r = random.random() if r < self.mutation_rate: gene = self.mutation_func(gene) self.mutation_count += 1 # 返回生命体 return Life(gene) # 根据得分情况,随机取得一个个体,机率正比于个体的score属性 def get_onelife(self): # 轮盘 r = random.uniform(0, self.bounds) for lf in self.lives: r -= lf.score; if r <= 0: return lf # 交叉函数:选择lf2序列前子序列交叉到lf1前段,删除重复元素 def overlapping_func(self, lf1, lf2): p2 = random.randint(1, self.gene_length - 1) # 截取if2 g1 = lf2.gene[0:p2] + lf1.gene g11 = [] for i in g1: if i not in g11: g11.append(i) return g11 # 变异函数:选择两个不同位置基因交换,第一个选择的基因重新加入到序列尾端 def mutation_func(self, gene): p1 = random.randint(0, self.gene_length - 1) p2 = random.randint(0, self.gene_length - 1) while p2 == p1: p2 = random.randint(0, self.gene_length - 1) gene[p1], gene[p2] = gene[p2], gene[p1] gene.append(gene[p2]) del gene[p2] return gene
完整的代码如下

1 # -*- coding: utf-8 -*- 2 3 import random 4 import math 5 6 class Life(object): 7 8 # 初始化 9 def __init__(self, gene = None): 10 self.gene = gene 11 self.score = -1.0 12 13 # 设置评估分数 14 def setScore(self, v): 15 self.score = v 16 17 18 #----------- TSP问题 ----------- 19 class MyTSP(object): 20 21 # 初始化 22 def __init__(self, gene_length = 28, overlapping_rate = 0.7, mutation_rate = 0.03, life_count = 30, max_iteration = 4000): 23 24 self.overlapping_rate = overlapping_rate # 交叉率 25 self.mutation_rate = mutation_rate # 突变率 26 self.mutation_count = 0 # 突变次数 27 self.generation = 0 # 进化代数 28 self.lives = [] # 生命集合 29 self.bounds = 0.0 # 得分总数 30 self.best = None # 种群每代中的最优个体 31 self.best_gene = [] # 所有代种群中的最优基因 32 self.best_gene_distance = 1e20 # 所有代种群中的最优基因所对应的路径长度 33 self.life_count = life_count # 生命个数 34 self.gene_length = gene_length # 基因长度,此处即为城市个数 35 self.max_iteration = max_iteration 36 self.min_distance = [] 37 38 # 创造生命集 39 for i in range(self.life_count): 40 self.lives.append(Life(self.make_life())) 41 42 # 读取各城市间的距离 43 with open('distance.txt', 'r') as f: 44 data = f.read() 45 data = data.replace(",", "") 46 odom = data.split() 47 self.dist_matrix = map(float, odom) 48 49 print self.lives[6].gene 50 print self.distance(self.lives[6].gene) 51 52 # 进化计算 53 def evolve(self): 54 while self.generation < self.max_iteration: 55 # 下一步进化 56 self.next() 57 self.min_distance.append(self.distance(self.best.gene)) 58 if self.distance(self.best.gene) < self.best_gene_distance: 59 self.best_gene_distance = self.distance(self.best.gene) 60 self.best_gene = self.best.gene 61 if self.generation % 200 == 0: 62 print("迭代次数:%d, 变异次数%d, 最佳路径总距离:%d" % (self.generation, self.mutation_count, self.distance(self.best.gene))) 63 print self.best_gene 64 print self.best_gene_distance 65 return 66 67 # 创造新生命 68 def make_life(self): 69 lst = range(self.gene_length) 70 # 随机顺序 71 random.shuffle(lst) 72 return lst 73 74 # 演化至下一代 75 def next(self): 76 # 评估群体 77 self.judge() 78 # 新生命集 79 newLives = [] 80 # 将最好的父代加入竞争 81 newLives.append(Life(self.best.gene)) 82 # 产生新的生命集个体 83 while(len(newLives) < self.life_count): 84 newLives.append(self.bear()) 85 # 更新新的生命集 86 self.lives = newLives 87 self.generation += 1 88 89 # 评价函数 90 def judge(self): 91 self.bounds = 0.0 92 self.best = Life() 93 self.best.setScore(-1.0) 94 for lf in self.lives: 95 lf.score = 1.0/self.distance(lf.gene) 96 if lf.score > self.best.score: 97 self.best = lf 98 self.bounds += lf.score 99 100 # 得到当前顺序下连线总长度 101 def distance(self, order): 102 distance = 0 103 for i in range(-1, self.gene_length - 1): 104 i1, i2 = order[i], order[i + 1] 105 distance += self.get_city_distance(self.dist_matrix, self.gene_length, i1, i2) 106 return distance 107 108 def get_city_distance(self, dist_matrix, n, i, j): 109 if i == j: 110 return 0 111 elif i > j: 112 i, j = j, i 113 return dist_matrix[i * (2 * n - i - 1)/2 + j - i - 1] 114 115 # 产生后代 116 def bear(self): 117 lf1 = self.get_onelife() 118 lf2 = self.get_onelife() 119 # 交叉 120 r = random.random() 121 if r < self.overlapping_rate: 122 gene = self.overlapping_func(lf1, lf2) 123 else: 124 gene = lf1.gene 125 # 突变 126 r = random.random() 127 if r < self.mutation_rate: 128 gene = self.mutation_func(gene) 129 self.mutation_count += 1 130 # 返回生命体 131 return Life(gene) 132 133 # 根据得分情况,随机取得一个个体,机率正比于个体的score属性 134 def get_onelife(self): 135 # 轮盘 136 r = random.uniform(0, self.bounds) 137 for lf in self.lives: 138 r -= lf.score; 139 if r <= 0: 140 return lf 141 142 # 交叉函数:选择lf2序列前子序列交叉到lf1前段,删除重复元素 143 def overlapping_func(self, lf1, lf2): 144 p2 = random.randint(1, self.gene_length - 1) 145 # 截取if2 146 g1 = lf2.gene[0:p2] + lf1.gene 147 g11 = [] 148 for i in g1: 149 if i not in g11: 150 g11.append(i) 151 return g11 152 153 # 变异函数:选择两个不同位置基因交换,第一个选择的基因重新加入到序列尾端 154 def mutation_func(self, gene): 155 p1 = random.randint(0, self.gene_length - 1) 156 p2 = random.randint(0, self.gene_length - 1) 157 while p2 == p1: 158 p2 = random.randint(0, self.gene_length - 1) 159 gene[p1], gene[p2] = gene[p2], gene[p1] 160 gene.append(gene[p2]) 161 del gene[p2] 162 return gene 163 164 165 import matplotlib.pyplot as plt 166 167 overlapping_rate = [0.1, 0.2, 0.3, 0.4, 0.5, 0.7, 0.8, 0.9, 1.0] 168 mutation_rate = [0.005, 0.01, 0.03, 0.05, 0.07, 0.1, 0.2, 0.4, 0.7, 1.0] 169 life_count = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] 170 yy = [] 171 172 for i in range(len(overlapping_rate)): 173 tsp = MyTSP(gene_length = 28, overlapping_rate = overlapping_rate[i], mutation_rate = 0.03, life_count = 30, max_iteration = 40) 174 tsp.evolve() 175 yy.append(tsp.best_gene_distance) 176 plt.figure('overlapping rate and minimum distance') 177 plt.plot(overlapping_rate, yy) 178 plt.xlabel('overlapping rate') 179 plt.ylabel("minimum distance of all generations") 180 181 yy = [] 182 for i in range(len(mutation_rate)): 183 tsp = MyTSP(gene_length = 28, overlapping_rate = 0.7, mutation_rate = mutation_rate[i], life_count = 30, max_iteration = 40) 184 tsp.evolve() 185 yy.append(tsp.best_gene_distance) 186 plt.figure("mutation rate and minimum distance") 187 plt.plot(mutation_rate, yy) 188 plt.xlabel('mutation rate') 189 plt.ylabel("minimum distance of all generations") 190 191 yy = [] 192 for i in range(len(life_count)): 193 tsp = MyTSP(gene_length = 28, overlapping_rate = 0.7, mutation_rate = 0.03, life_count = life_count[i], max_iteration = 40) 194 tsp.evolve() 195 yy.append(tsp.best_gene_distance) 196 plt.figure('life count of population and minimum distance') 197 plt.plot(life_count, yy) 198 plt.xlabel('life count of population') 199 plt.ylabel("minimum distance of all generations") 200 201 yy = [] 202 tsp = MyTSP(28, 0.5, 0.03, 30, 40) 203 tsp.evolve() 204 plt.figure('number of generation and minimum distance') 205 plt.plot(range(1, tsp.max_iteration + 1), tsp.min_distance) 206 plt.xlabel('number of generation') 207 plt.ylabel("minimum distance of every generation") 208 209 plt.show()
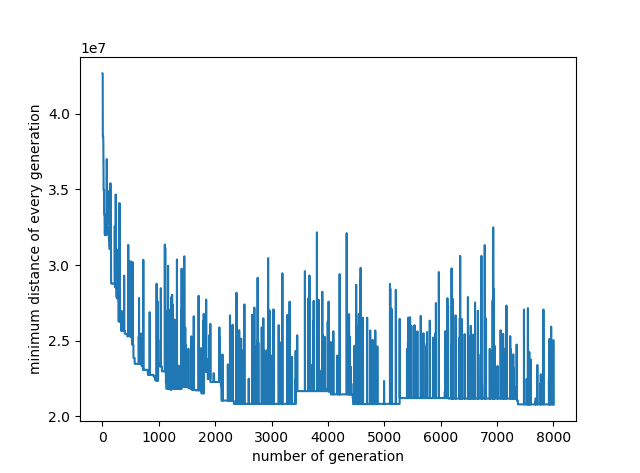
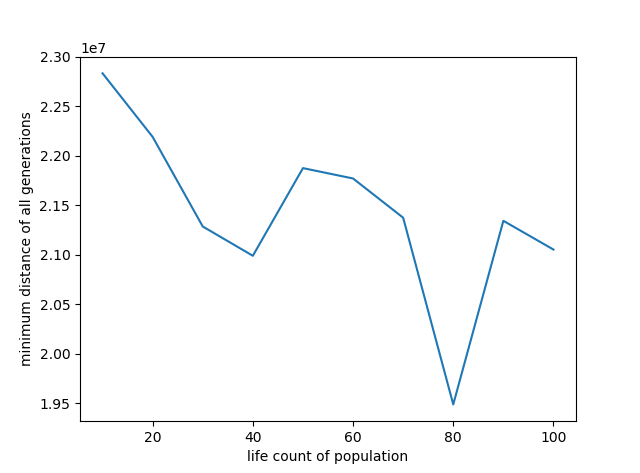
代码中探究了迭代次数、交叉概率、变异概率、种群中生命体个数对求解效果的影响,分别如下面的4张曲线图