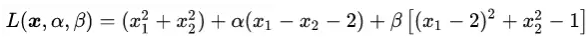有约束条件的最优化模型

优化问题：

所有优化问题都可以形式化成 

minimize ƒ₀(x), x€Rⁿ

st. f_i(x)<=0

　h_i(x) =0                i = 1,2,3,...m

如果 ƒ₀(x)为凸函数， ƒi(x)为凸函数，hi（x）为仿函数，则该优化问题为凸优化问题

约束条件：

1.等式约束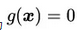        

 2.不等式约束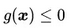由于KKT条件，所以需要有等号

上确界（Supremum）：一个集合的最小上界， 数学符号sup

下确界（greatest lower boundinf）：一个集合的最大下界,数学符号inf

上确界与最大值：上确界类似于最大值，但是和最大值不同的是，最大值有时候会遇到无法取到的情况。比如x∈R,x<2这样的情况下就不存在一个确定的最大值。但是可以确定上确界为2。

下确界与最小值:参考上面

几何想象：

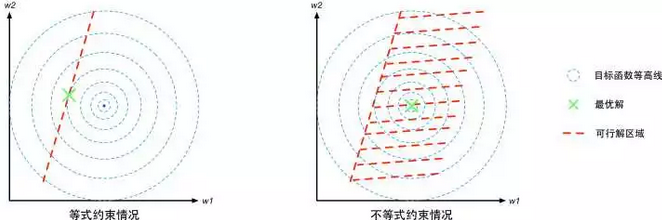
（图中的目标函数等高线其实就是等值线，在同一条等值线上的点对应的目标函数值相同）。

假设（就是这个向量一共有d个标量组成），则的几何意象就是d维空间中的d-1维曲面，如果函数是线性的，则是个d-1维的超平面（这是平面中的直线、空间中的平面之推广（n大于3才被称为“超”平面））。那么有约束优化问题就要求在这个d-1维的曲面或者超平面上找到能使得目标函数最小的点，这个d-1维的曲面就是“可行解区域”。

对于不等式约束条件，，则可行解区域从d-1维曲面扩展成为d维空间的一个子集。我们可以从d=2的二维空间进行对比理解。等式约束对应的可行解空间就是一条线；不等式约束对应的则是这条线以及线的某一侧对应的区域。

拉格朗日乘子法：

将有等式约束优化问题转为无约束优化问题，形式如下：

、

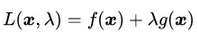目标函数有两个自变量 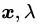，分别对两变量取导数，等式取0。

KKT条件：

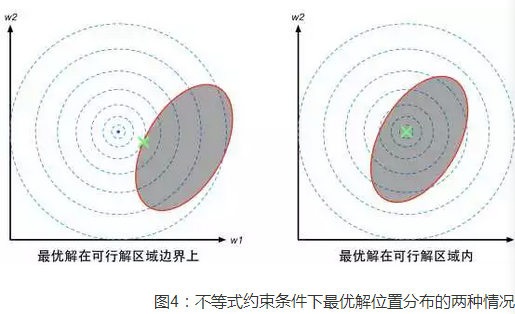
对于不等式约束条件，最优解可能有两种情况

（1）最优解在边界上，就相当于约束条件就是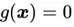，所以函数 f(x)在最优解x*附近的变化趋势是“在可行解区域内侧较大而在区域外侧较小”，与之对应的是函数g(x)在可行解区域内小于0，在区域外大于零，所以在最优解x*附近的变化趋势是内部较小而外部较大。这意味着目标函数f(x)的梯度方向与约束条件函数g(x)的梯度方向相反。因此根据拉格朗日公式，可以推断出参数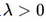

（2）如果在区域内，则相当于约束条件没有起作用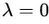

整合上述两种情况：

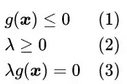
（1）是约束条件 （2）是拉格朗日乘子的描述（3）是两种情况的推论，在第一种情况里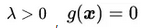，；在第二种情况下，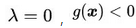

Karush-Kuhn-Tucker条件从约束条件（1）扩展出另外两个条件，原因是：

1）KKT条件是对最优解的约束，而原始问题中的约束条件是对可行解的约束。

2）KKT条件的推导对于拉格朗日对偶问题的推导很重要。

对偶问题

提出问题：构造拉格朗日方程的目的是将约束条件放到目标函数中，从而将有约束优化问题转换为无约束优化问题。那么如何针对不等式约束条件下的优化问题构建拉格朗日函数呢？

如果能够构造一个函数，使得该函数在可行解区域内与原目标函数完全一致，而在可行解区域外的数值非常大，甚至是无穷大，那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化是等价的问题。

（1）原始目标函数

m个等式约束条件和n个不等式约束条件的目标函数f（x）的优化问题

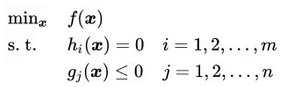
（2）构造没有约束条件的目标函数

目标是建立一个在可行解区域内与原目标函数相同，在可行解区域外函数值趋近于无穷大的新函数

基于广义拉格朗日函数L的新目标函数：

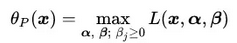
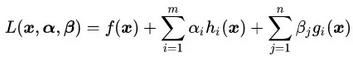
其中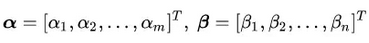，是针对等式约束和不等式约束的系数变量

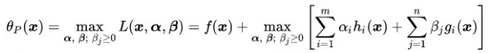
 （3）对偶问题

 L函数很难把alpha和beta变量拿掉，单纯令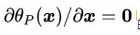来求解最优解x*，这里就引入了对偶概念

原不带约束条件的目标函数可以表达为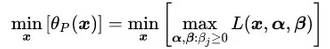其中，P是原始问题Primary的缩写

构造新函数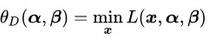

得到对偶等式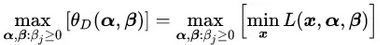其中，D是对偶问题Dual的缩写

对偶式可以被证明与原目标式具有相同解 x* alpha* beta*

可视化案例

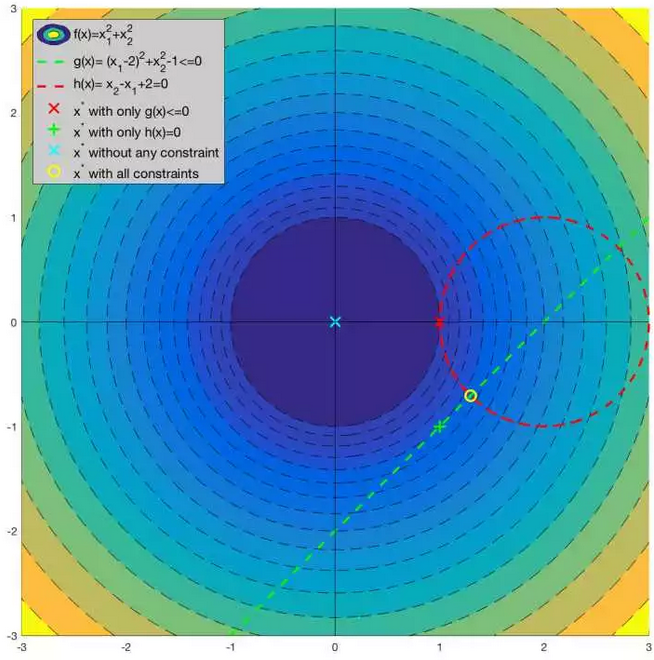
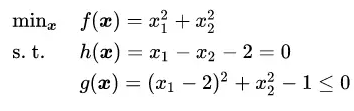
如果没有任何约束条件，最优解在坐标原点(0, 0)处（青色X）；如果只有不等式约束条件 ，最优解在坐标(1,0)处（红色X）；如果只有等式约束条件 ，在坐标(1,-1)处（绿色+）；如果两个约束条件都有，最优解在黄色处。

构建拉格朗日函数