斐波拉契数列的元素是：1，1，2，3，5，8，13，…等
本例中以四种不同的方式来实现：
方法1：递归方法实现
代码：
#include<iostream>
#include<cmath>
using namespace std;
int f1(int i)
{
if (i == 0 || i == 1)
{
return 1;
}
else
{
return f1(i - 1) + f1(i - 2);
}
}
int main()
{
cout << "=============使用递归算法============";
const int n =20;
int f[n] = { 1, 1 };
int i = 0;
for (i = 2; i < n; i++)
{
f[i] = f1(i);
}
print(f, n);
return 0;
结果：
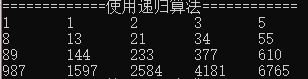
在本段代码中，我们定义了一个计算斐波拉契数列各项元素的函数，然后将这个函数的返回值赋值给存放斐波拉契数列元素的一个数组。斐波拉契数列的特点是：从第三项开始，每一项都等于前两项之和。因此，当项数为1，2时，即数组中下标为0，1时，返回值为1，这就是斐波拉契数列的前两项。当项数大于2时，每一项等于前两项之和，返回值为f1(i - 1) + f1(i - 2)。上述就是用递归来实现斐波拉契数列的方法，不难发现，在递归的过程中，有很多重复性计算的项，程序的效率很低。我们来看下面一种方法。
方法2：
代码：
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
int f[n] = { 1, 1 };
int i = 0;
for (i = 2; i < n; i++)
{
f[i] = f[i - 1] + f[i -2];
}
print(f, n);
return 0;
}
结果：
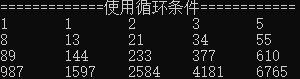
在这种方法中，我们采用了通过循环来计算斐波拉契数列的各项。我们预先定义了前两项分别为1，1。从第三项开始，每一项等于前两项之和，逐次地计算出第3项，第4项，直到第20项。相比于递归，这种方法效率更高。
方法3：通项公式法
代码：
#include<iostream>
#include<cmath>
using namespace std;
int f2(int i)
{
int temp;
double v1, v2;
v1 = (sqrt(5) + 1) / 2, v2 = (1 - sqrt(5)) / 2;
temp = (powl(v1, i+1) - powl(v2, i+1)) / sqrt(5);
return temp;
}
int main()
{
cout << "=============使用通项公式============";
for (i = 0; i < n; i++)
{
f[i] = f2(i);
}
print(f, n);
return 0;
}
结果：
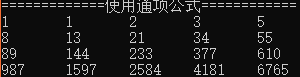
斐波拉契数列数列的通项公式为：
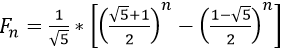，使用这个公式可以直接计算出数列的每一项。关于这个公式的推导可以有多种方法，这里不细表。
方法4：使用矩阵计算
斐波拉契数列可以写成如下形式：
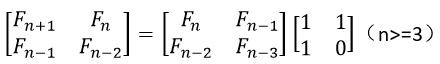
因此，可以利用二维数组来计算和表示斐波拉契数列。
代码：
#include<iostream>
#include<cmath>
using namespace std;
void f3(int a[], int n)
{
int m1[2][2] = { { 1, 1 }, { 1, 0 } };
int m2[2][2] = { { 3, 2 }, { 1, 1 } };
int m3[2][2] = { 0, 0, 0, 0 };
for (int k = 2; k < n - 2; k++)
{
m3[0][0] = m2[0][0] * m1[0][0] + m2[0][1] * m1[1][0];
m3[0][1] = m2[0][0] * m1[0][1] + m2[0][1] * m1[1][1];
m3[1][0] = m2[1][0] * m1[0][0] + m2[1][1] * m1[1][0];
m3[1][1] = m2[1][0] * m1[0][1] + m2[1][1] * m1[1][1];
a[k] = m3[1][0];
a[k + 1] = m3[0][1];
a[k + 2] = m3[0][0];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < 2; j++)
m2[i][j] = m3[i][j];
}
}
}
int main()
{
const int n =20;
int f[n] = { 1, 1 };
int i = 0;
cout << "=============使用矩阵乘法============";
f3(f, n);
print(f, n);
return 0;
}
结果:
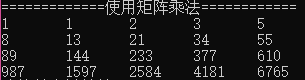
如式（n>=3）所示，每次可以根据这个公式计算出一个矩阵，然后将其赋值给矩阵m2，计算下一项时，用m2与矩阵相乘。如结果所示，这样同样能够得到斐波拉契数列。