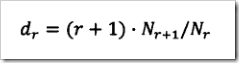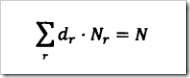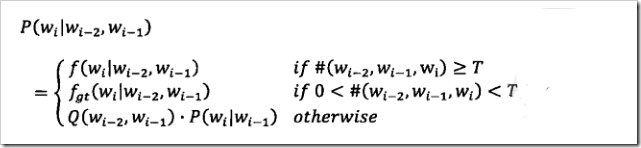延伸阅读：
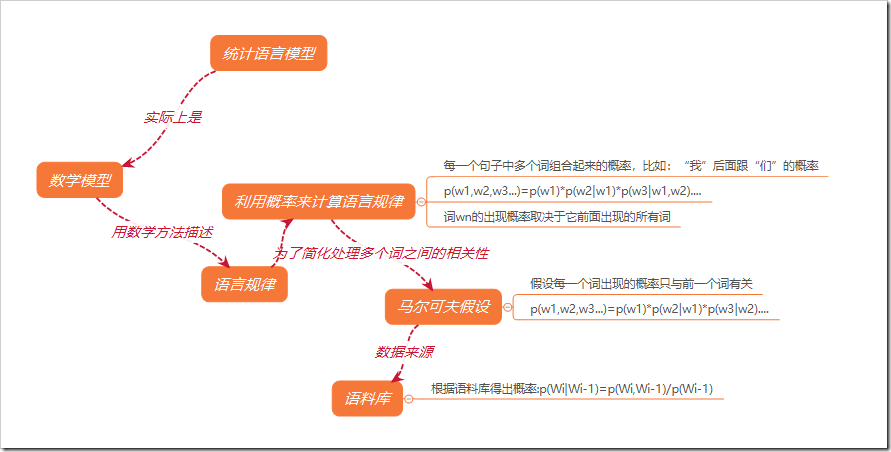
1.N-1阶马尔可夫假设：
2.零概率和平滑方法：
假定在语料库中出现r次的词有Nr个，未出现的词数为N0，语料库的大小为N。那么显然：
出现r次的词在整个语料库中的相对频度则是r/N，如果不做任何优化处理，就是这个相对频度作为这些词的概率估计。
现在假定当r比较小时，它的统计可能不可靠，因此出现r次的那些词在计算它们概率时要使用一个更小一点的次数，是dr（而不直接使用r），古德-图灵估计按照下面的公式计算dr。
显然
（公式的由来可以参考下面的定律）
一般来说，出现一次的词数量比出现两次的多，出现两次的比出现三次的多，这种规律称为Zipf定律。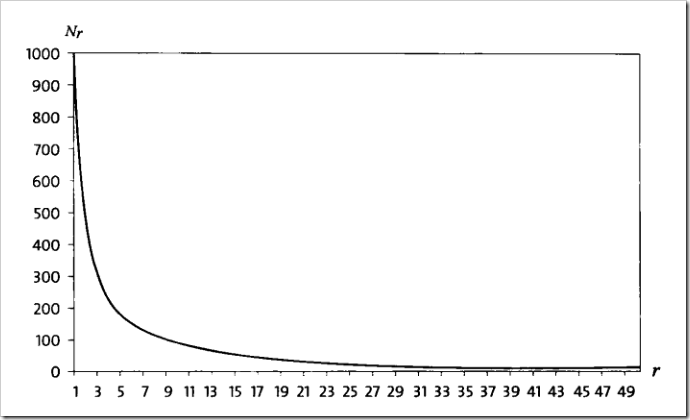
Nr+1<Nr，因此一般情况下dr<r,这样就给未出现的词赋予了一个非常小的的非零值，从而解决了零概率的问题。
对于未看见的词，也给予了一个比较小的概率，这样所有词的概率估计都很平滑了。
对于二元组（wi-1,wi）的概率估计P（wi|wi-1）也可以做同样的处理。
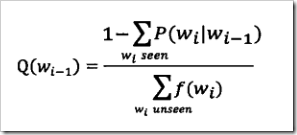
二元模型概率的公式如下：
注意：T为某一阀值,fgt()表示经过古德-图灵估计后的相对频度，而
对于三元模型，概率估计公式如下：
3.语料的选取问题：
