关于路径存储的常见优化——前向星与链式前向星
我们在做搜索和动规题目时,一般用到的是邻接矩阵或者邻接表
由于邻接矩阵占用空间过大、邻接表需要调用vector过于繁杂
所以在图论学习时,我们需要引入一类新的存储方式:前向星
前向星
前向星是一种存储有关边的数据的存储方式
一般储存的是:第 i 条边的起点,第 i 边的终点,第 i 边的边权
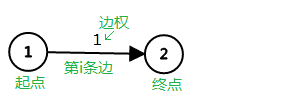
struct node{
int from;//某条边的起点
int to;//某条边的终点
int l;//某条边的边权
}edge[1010];
然后我们进行读入数据
但前向星仍会会有一些不足
比如,需要在所有边都读入完毕的情况下对所有边进行一次排序
bool cmp(node x,node y){
return x.form<y.form;
}
int main(){
sort(edge,edge+m,cmp)//排序
return 0;
}
为什么要进行排序呢?为了方便我们在后面对起点进行操作
所以这是一种用时间换空间的做法
比如我们现在举个例子:
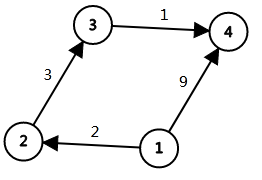
如图,数据输入顺序如下
1 2 2
3 4 1
2 3 3
1 4 9
我们将数据存入前向星得到
| i | from | to | l |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 3 | 4 | 3 |
| 3 | 2 | 3 | 3 |
| 4 | 1 | 4 | 9 |
然后排序后得到
| i | from | to | l |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 1 | 4 | 9 |
| 3 | 2 | 3 | 3 |
| 4 | 3 | 4 | 3 |
利用前向星会有排序操作,那该如何解决呢?
还能做到更优吗?
链式前向星
提到链式前向星,你会联想到什么?
链表?前向星?
都对,综合一下,其实链式前向星就是用数组模拟链表的一种对前向星的优化
虽说鱼和熊掌不可得兼,但链式前向星真正意义上做到了优化空间占用又减少时间占用
因为它避免了对数据的排序
那它是怎么做到的呢?我认为这是巧妙、有趣的
同样,链式前向星会定义:第 i 边的终点,第 i 边的边权
但第 i 条边的起点会和 i(边编号) 被当做数组模拟链表的指针使用
链表是一种存储上非连续、非顺序的存储结构
所以我们利用这一点无需排序
具体怎么做呢?
首先定义储存结构:
struct node{
int next;//这条边同起点的上一条边的位置
int to;//这条边的终点
int l;//这条边的边权
}edge[1010];
int head[1010];//这条边所在起点的最后一条边
l 和 to 的含义都是不变的,表示第 i 条边的终点和第 i 边的边权
而 next 表示的是与第 i 条边相邻的一条同起点边,相当于链表的子指针
head是作为记录的是以第 i 条边所在起点为起点的首条边,相当于链表的头指针
(这个地方很巧妙,记录的是上一条条边的位置和最后一条边的位置,稍后会讲到)
首先我们输入和存储 to 和 l没有任何疑问,和前向星一致,而form我们先暂时用临时变量x表示
于是:
int main(){
for(int i=0;i<m;i++){
cin>>x>>y>>z;
edge[i].to=y;
edge[i].l=z;
}
return 0;
}
然后我们对next和head进行处理
memset(head,-1,sizeof(head));
先对head进行初始化,由于我们是从i=0开始存储的,所以head赋值为-1
否则模拟链表的最后一个元素会指向一些奇奇怪怪的地方
来看一下代码
int main(){
for(int i=0;i<m;i++){//边的编号i
cin>>x>>y>>z;//i条边的起点,终点,边权
edge[i].next =head[x];//黑色箭头为其赋值(1),绿色箭头表示指向(2)
edge[i].to =y;
edge[i].l =z;
head[x]=i; //红色数据表示更新(3),蓝色箭头表示指向(4)
}
}
举一组数据:
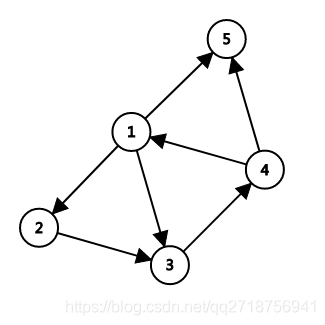
1 2
2 3
3 4
1 3
4 1
1 5
4 5
初始应该为:
| i(边的编号) | to(边的终点) | next(同起点的临边的编号,子指针) | head(所在起点最开始的边的编号,头指针) |
|---|---|---|---|
| 0 | 2 | -1 | 0 |
| 1 | 3 | -1 | 1 |
| 2 | 4 | -1 | 2 |
| 3 | 3 | 0 | 3 |
| 4 | 1 | -1 | 4 |
| 5 | 5 | 3 | 5 |
| 6 | 5 | 4 | 6 |
然后我们依次操作后
这样按照程序操作:
 (注意,head[x]是指x为起点的最后一条边)
(注意,head[x]是指x为起点的最后一条边)
得到存储:
| i(边的编号) | to(边的终点) | next(同起点的临边的编号,子指针) | head(所在起点最开始的边的编号,头指针) |
|---|---|---|---|
| 0 | 2 | -1 | 5 |
| 1 | 3 | -1 | 1 |
| 2 | 4 | -1 | 2 |
| 3 | 3 | 0 | 5 |
| 4 | 1 | -1 | 6 |
| 5 | 5 | 3 | 5 |
| 6 | 5 | 4 | 6 |
也就是一个数组模拟链表的的图
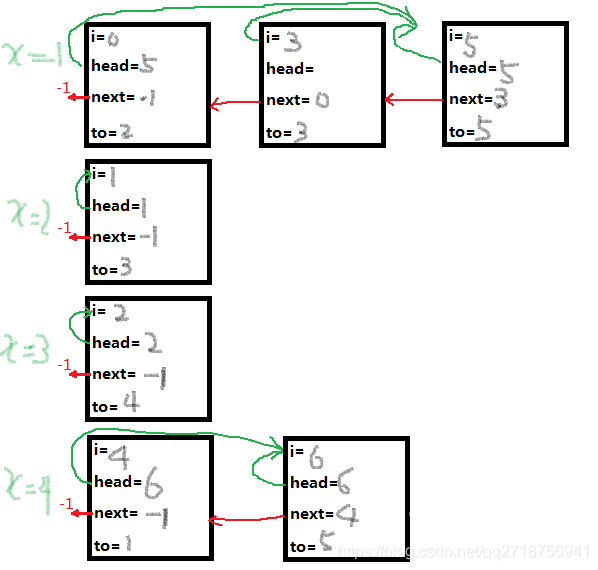 我们就不难发现,巧妙之处在于
我们就不难发现,巧妙之处在于
从开始向后输入数据,head[X]的值可能会再次刷新
所以head其实存储的是以X为起点的最后一条边,next是自后向前连接
这个模拟链表是以x为起点从最后一条边向前连接
避免了X为起点的第一条边向后连接的许多麻烦
所以,大致代码为:
#include<bits/stdc++.h>
using namespace std;
struct node{
int next;//这条边同起点的上一条边的位置
int to;//这条边的终点
int l;//这条边的边权
}edge[1010];
int head[1010];//这条边所在起点的最后一条边
int main(){
cin>>m;
for(int i=0;i<m;i++){//边的编号i
cin>>x>>y>>z;//i条边的起点,终点,边权
edge[i].next =head[x];//黑色箭头为其赋值(1),绿色箭头表示指向(2)
edge[i].to =y;
edge[i].l =z;
head[x]=i; //红色数据表示更新(3),蓝色箭头表示指向(4)
}
//其他操作......
return 0;
}
总结
总结一下,前向星和链式前向星都是对边进行存储
均对空间进行优化,均需要存储终节和视情况存储边权
前向星需要对边进行排序,要在结构体中单独存储边的起点X
而链式前向星则是用数组模拟链表的方式避免了耗时的排序
用head储存起点X的最后一条边,作为头指针;next从后向前指向,作为子指针
多使用一个head数组,但仍是优化了空间,也不浪费时间
推荐在数据较大时候,使用链式前向星,以达到不会在排序时浪费更多时间从而避免超时的目的
但前向星由于写法更加简单,可以在一些数据不大的情况下使用
--END--