1.顺序查找
- 当数据存储在诸如列表的集合中时,我们说这些数据具有线性或顺序关系。 每个数据元素都存储在相对于其他数据元素的位置。 由于这些索引值是有序的,我们可以按顺序访问它们。 这个过程产实现的搜索即为顺序查找。
- 顺序查找原理剖析:
- 从列表中的第一个元素开始,我们按照基本的顺序排序,简单地从一个元素移动到另一个元素,直到找到我们正在寻找的元素或遍历完整个列表。如果我们遍历完整个列表,则说明正在搜索的元素不存在。
- 代码实现:该函数需要一个列表和我们正在寻找的元素作为参数,并返回一个是否存在的布尔值。found 布尔变量初始化为 False,如果我们发现列表中的元素,则赋值为 True。
1 def search(alist,item): 2 find = False 3 cur = 0 4 while cur < len(alist): 5 if alist[cur] == item: 6 find = True 7 break 8 else: 9 cur += 1 10 return find
2.二分查找
- 有序列表对于我们的实现搜索是很有用的。在顺序查找中,当我们与第一个元素进行比较时,如果第一个元素不是我们要查找的,则最多还有 n-1 个元素需要进行比较。
- 二分查找则是从中间元素开始,而不是按顺序查找列表。 如果该元素是我们正在寻找的元素,我们就完成了查找。 如果它不是,我们可以使用列表的有序性质来消除剩余元素的一半。
如果我们正在查找的元素大于中间元素,就可以消除中间元素以及比中间元素小的一半元素。如果该元素在列表中,肯定在大的那半部分。然后我们可以用大的半部分重复该过程,继续从中间元素开始,将其与我们正在寻找的内容进行比较。
1 def search(alist,item): 2 left = 0 3 right = len(alist) - 1 4 find = False 5 6 while left <= right: 7 mid_index = (left + right)//2 8 if item == alist[mid_index]: 9 find = True 10 break 11 else: 12 if item > alist[mid_index]: 13 left = mid_index + 1 14 else: 15 right = mid_index -1 16 17 return find
3.冒泡排序
原理:
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

1 def sort(alist): 2 length = len(alist) 3 for i in range(0,length-1): 4 for j in range(0,length-1-i): 5 if alist[i] > alist[i+1]: 6 alist[i],alist[i+1] = alist[i+1],alist[i]
4.选择排序
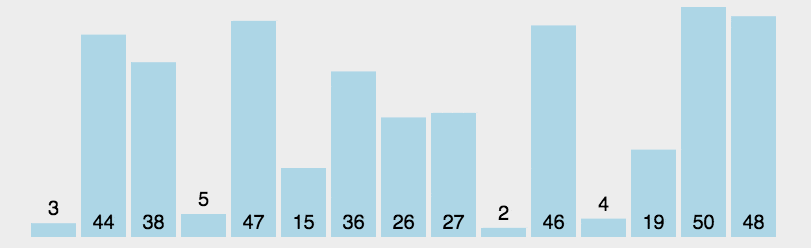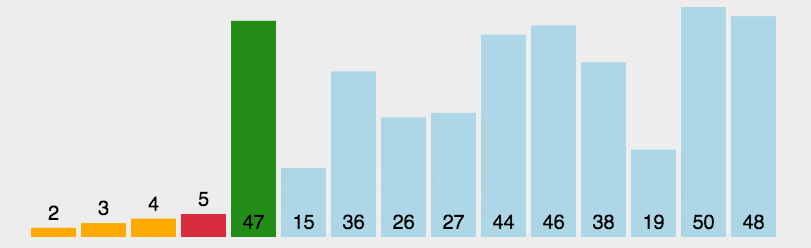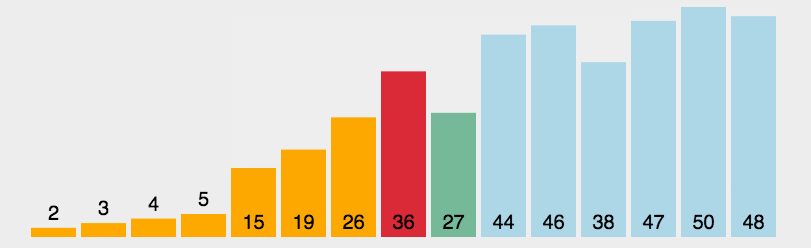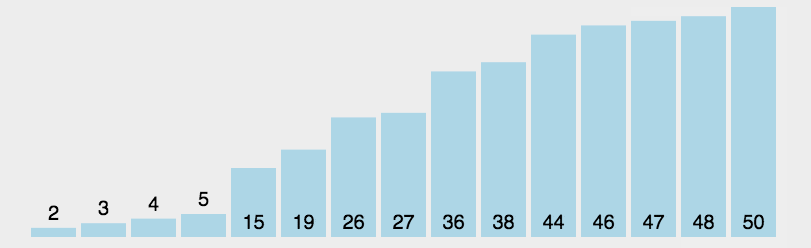
工作原理:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
1 def sort(alist): 2 length = len(alist) 3 for j in range(length-1,0,-1): 4 max_index = 0 5 for i in range(1,j+1): 6 if alist[max_index] < alist[i]: 7 max_index = i 8 alist[max_index],alist[j] = alist[j],alist[max_index] 9
5.插入排序
原理:
基本思想是,每步将一个待排序的记录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。关键码是数据元素中某个数据项的值,用它可以标
示一个数据元素。
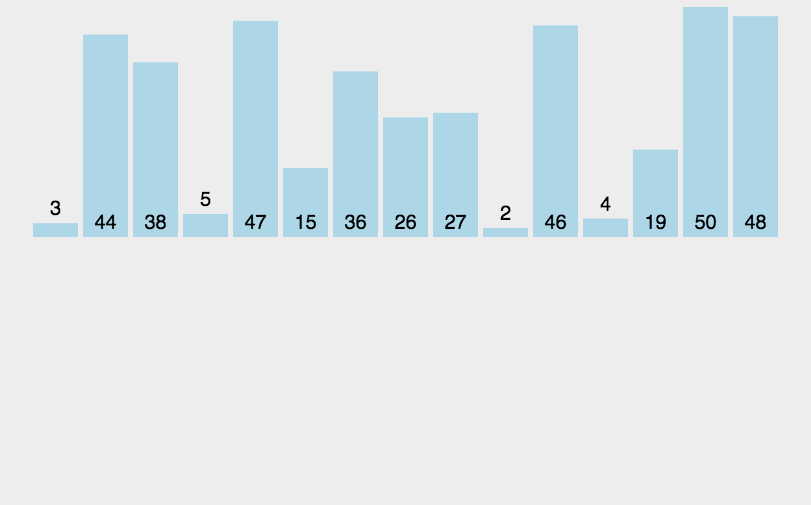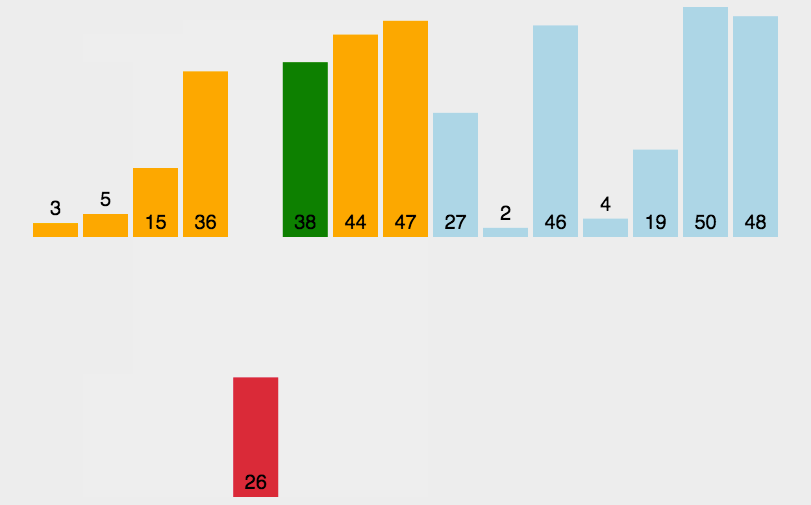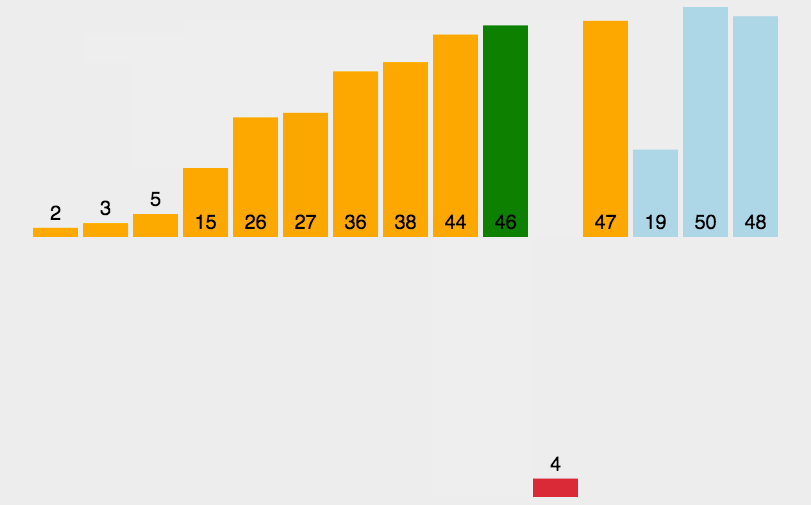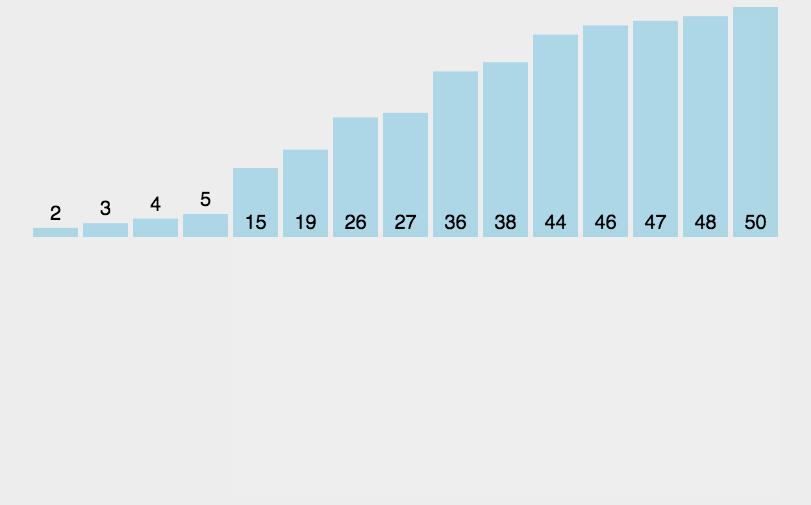
1 def sort(alist): 2 length = len(alist) 3 for j in range(1,length): 4 i = j 5 while i > 0: 6 if alist[i] < alist[i-1]: 7 alist[i],alist[i-1] = alist[i-1],alist[i] 8 i -= 1 9 else: 10 break 11
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量(gap)”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率比直接插入排序有较大提高。
1 def sort(alist): 2 gap = len(alist)//2 3 while gap >= 1: 4 for j in range(gap,len(alist)): 5 i = j 6 while i > 0: 7 if alist[i] < alist[i-gap]: 8 alist[i],alist[i-gap] = alist[i-gap],alist[i] 9 i -= gap 10 else: 11 break 12 gap = gap // 2
6.快速排序
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。

1 def sort(alist,start,end): 2 low = start 3 high = end 4 if low >= high: 5 return 6 mid = alist[low] 7 while low < high: 8 while low < high: 9 if alist[high] >= mid: 10 high -= 1 11 else: 12 alist[low] = alist[high] 13 break 14 while low < high: 15 if alist[low] < mid: 16 low += 1 17 else: 18 alist[high] = alist[low] 19 break 20 alist[low] = mid 21 sort(alist,start,low-1) 22 sort(alist,high+1,end)
7.归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。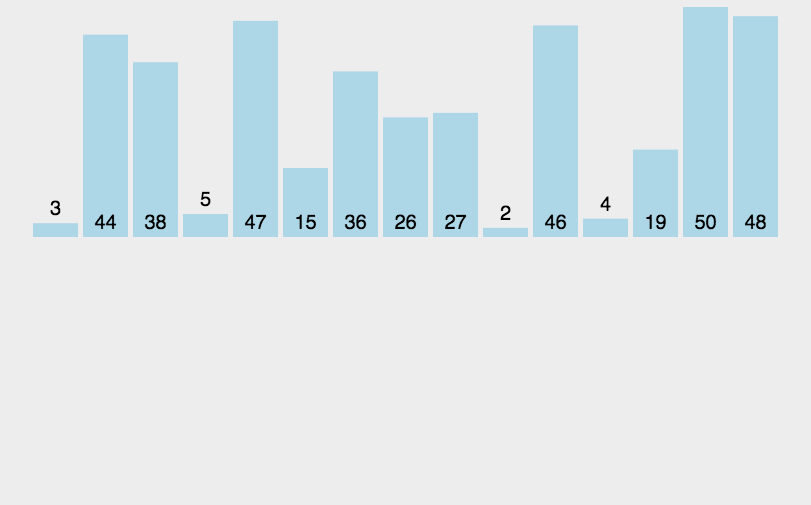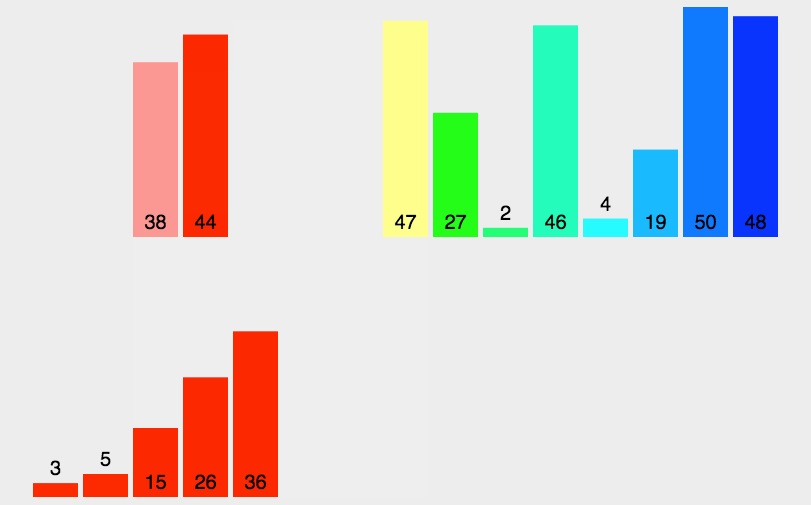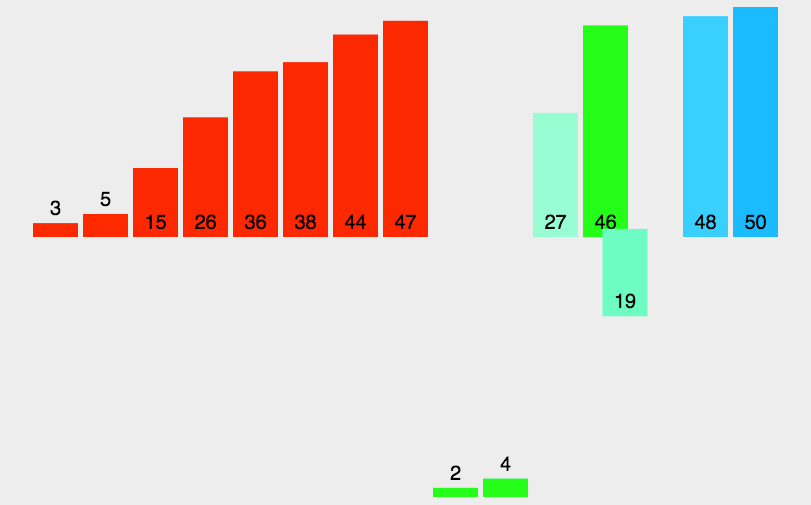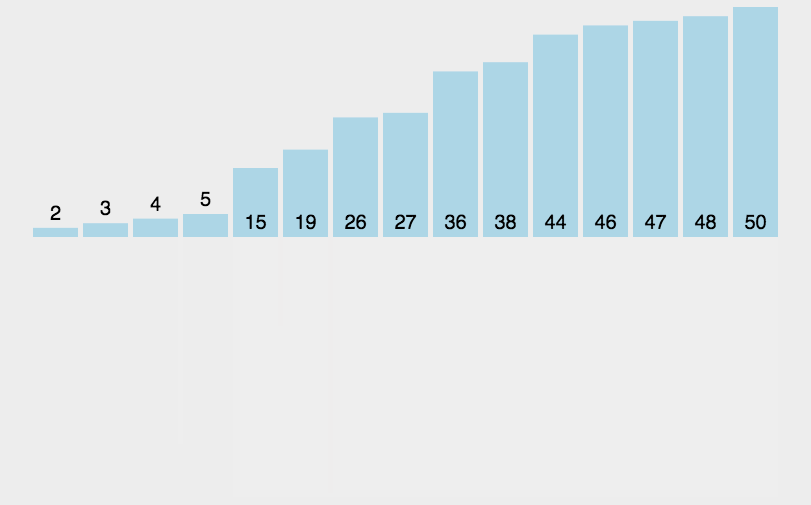
1 def merge_sort(alist): 2 n = len(alist) 3 #结束递归的条件 4 if n <= 1: 5 return alist 6 #中间索引 7 mid = n//2 8 9 left_li = merge_sort(alist[:mid]) 10 right_li = merge_sort(alist[mid:]) 11 12 #指向左右表中第一个元素的指针 13 left_pointer,right_pointer = 0,0 14 #合并数据对应的列表:该表中存储的为排序后的数据 15 result = [] 16 while left_pointer < len(left_li) and right_pointer < len(right_li): 17 #比较最小集合中的元素,将最小元素添加到result列表中 18 if left_li[left_pointer] < right_li[right_pointer]: 19 result.append(left_li[left_pointer]) 20 left_pointer += 1 21 else: 22 result.append(right_li[right_pointer]) 23 right_pointer += 1 24 #当左右表的某一个表的指针偏移到末尾的时候,比较大小结束,将另一张表中的数据(有序)添加到result中 25 result += left_li[left_pointer:] 26 result += right_li[right_pointer:] 27 28 return result 29 30 alist = [3,8,5,7,6] 31 print(merge_sort(alist))
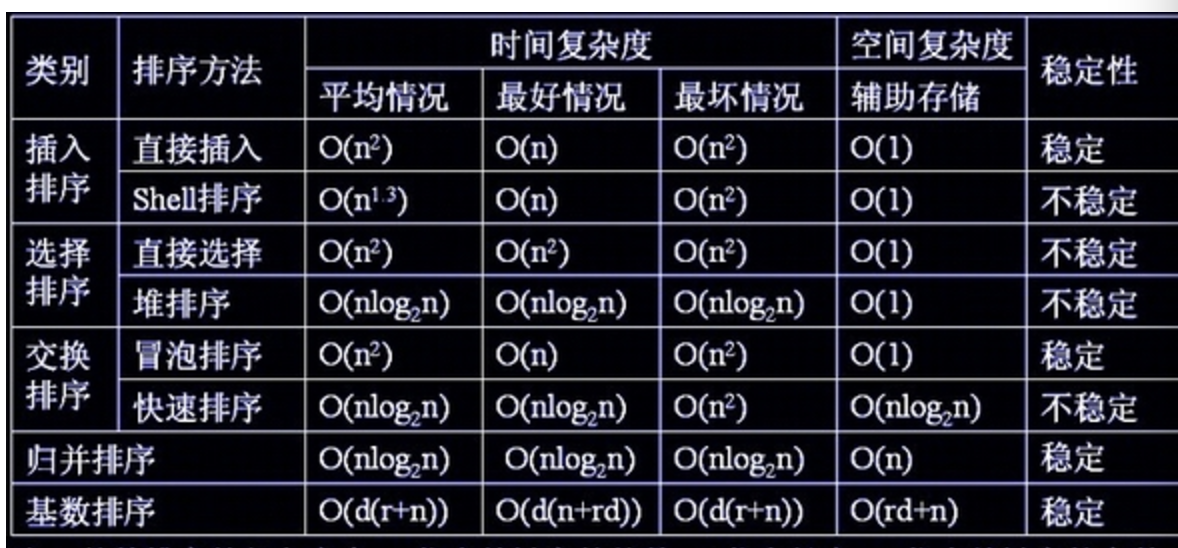
8.各个算法的时间复杂度