算法思想:
1.将用户对物品的反馈记录,转换为2分图
2.使用随机游走算法,计算从用户节点u到物品节点i的概率,作为用户对物品的喜好
(2分图)例子:
| 数据集 | 2分图 | ||||||||||
|
 |
(随机游走)分析:
比如从A点出发,每一步,有$alpha$的概率继续往下走,$1-alpha$的概率返回A
如果将所在位置的概率表示为向量,则初始向量为 $r_0=(1,0,0,0,0,0) $对应(A,B,C,a,b,c),
经过第一步后,$r=(1-alpha,0,0,0.5,0.5,0)$
根据 ,构建矩阵
,构建矩阵

可以知道: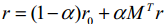 ,经过迭代后最终收敛,
,经过迭代后最终收敛,
求得到
代码:
def PersonalRank(G, alpha, root): rank = {x:0 for x in G.keys()} rank[root]=1 for i in range(20): tmp = {x:0 for x in G.keys()} for node,rk in rank.items(): paths=G[node] for path in paths: tmp[path] += alpha*rk/len(paths) tmp[root] += (1-alpha) rank = tmp return rank record=[('A','a'),('A','b'),('B','a'),('B','c'),('C','b')] g = {} for rec in record: if rec[0] not in g: g[rec[0]]=set() g[rec[0]].add(rec[1]) if rec[1] not in g: g[rec[1]]=set() g[rec[1]].add(rec[0]) print PersonalRank(g,0.9,'A')