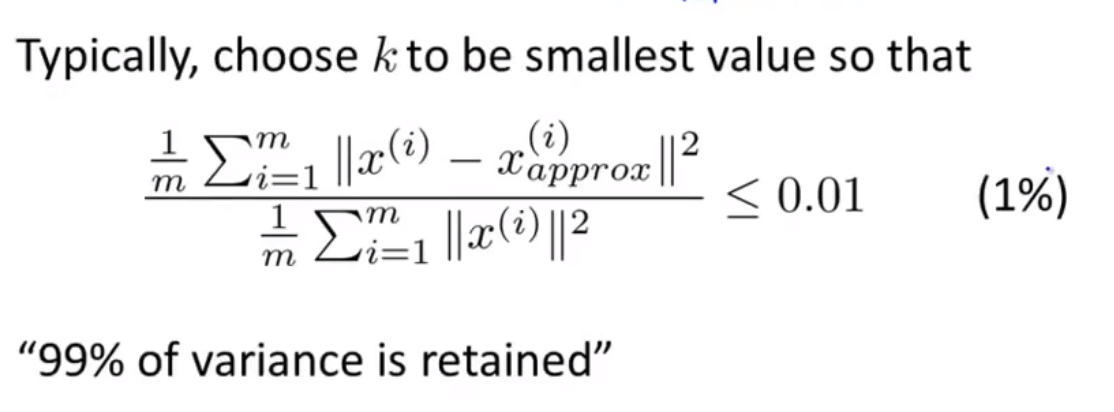主成分分析法(PCA)
PCA的思想
降维的作用
- 数据压缩
- 加速学习算法
- 可视化
PCA的思想: 试图找到一个低维的平面,来对高维数据进行投影,以便最小化投影误差的平方,以及最小化每一个点与投影后的点之间的距离的平方值.
一个PCA的直观理解: 将二维空间映射到一维空间上
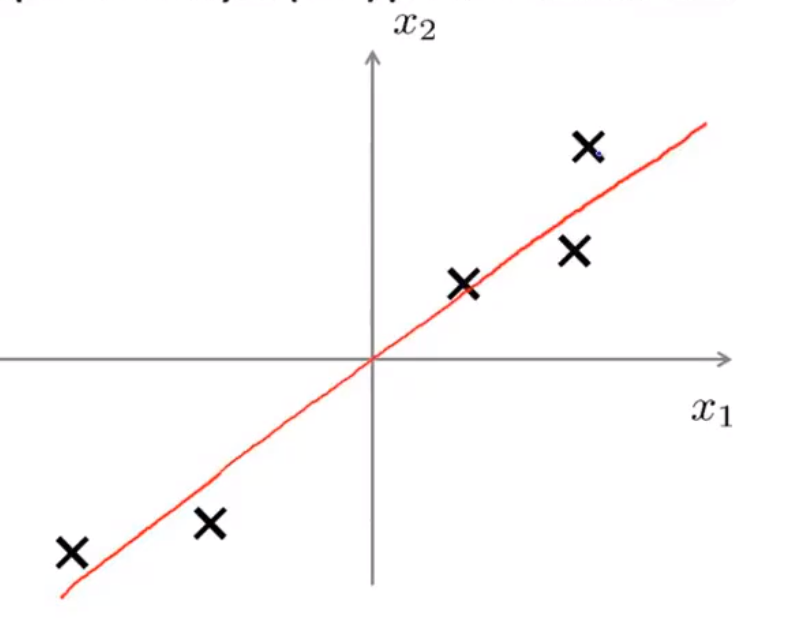
如何理解降维: 对于本图,如果我们将每一个点朝着红色直线作垂线投影,那么就可以通过直线上的向量长度来区别每个点.
这种投影方式会忽略掉点到直线的垂直距离的大小,因此如果存在两个点的连线垂直于这条红线,那么这就不是一个非常优秀的降维(重构误差较大)
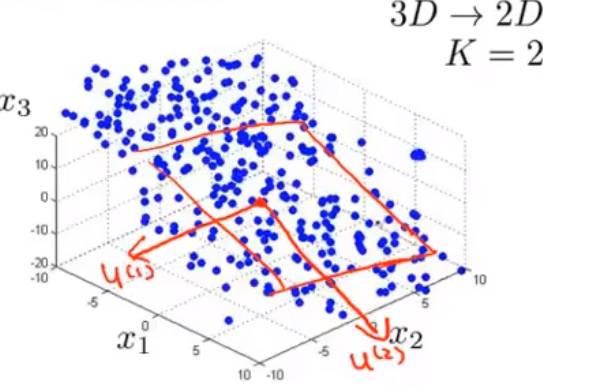
更加高级的应用: 将 n 维空间映射到 k 维空间上,那么就需要找到k个向量作为基底,此时每个点都可以近似表示为这k个线性无关的向量的线性组合. 如图找到两个2维向量作基底,映射3维数据的例子
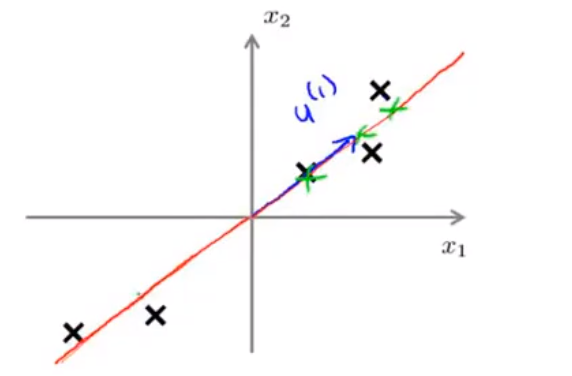
在使用PCA时,我们希望每一个样本点到达投影面的距离都尽量地小,这有利于缩小重构误差.
PCA的实现
- step1: 数据预处理
在进行PCA之前,首先需要对数据进行预处理,常用的数据预处理手段包括: 标准化,归一化,特征缩放

- step2:
假设我们想把n维数据降到k维数据,我们首先需要计算一个协方差矩阵(covariance matrix)
[Sigma = frac{1}{m}sum_{i=1}^{m}(x^{(i)})(x^{(i)})^T
]
这是一个n*n矩阵(X是n*m矩阵,(x^{(i)})是X的第i列向量,规模为(n*1))
对于matlab和ocatave,使用如下代码进行计算
% X: n*m
Sigma = 1/m * X * X';
[U,S,V] = svd(Sigma);
% svd是奇异值分解,对于这三个输出值,我们只需要结果U,它同样是一个n*n矩阵; 如果我们想将n维降到k维,只需要取前k个列向量;
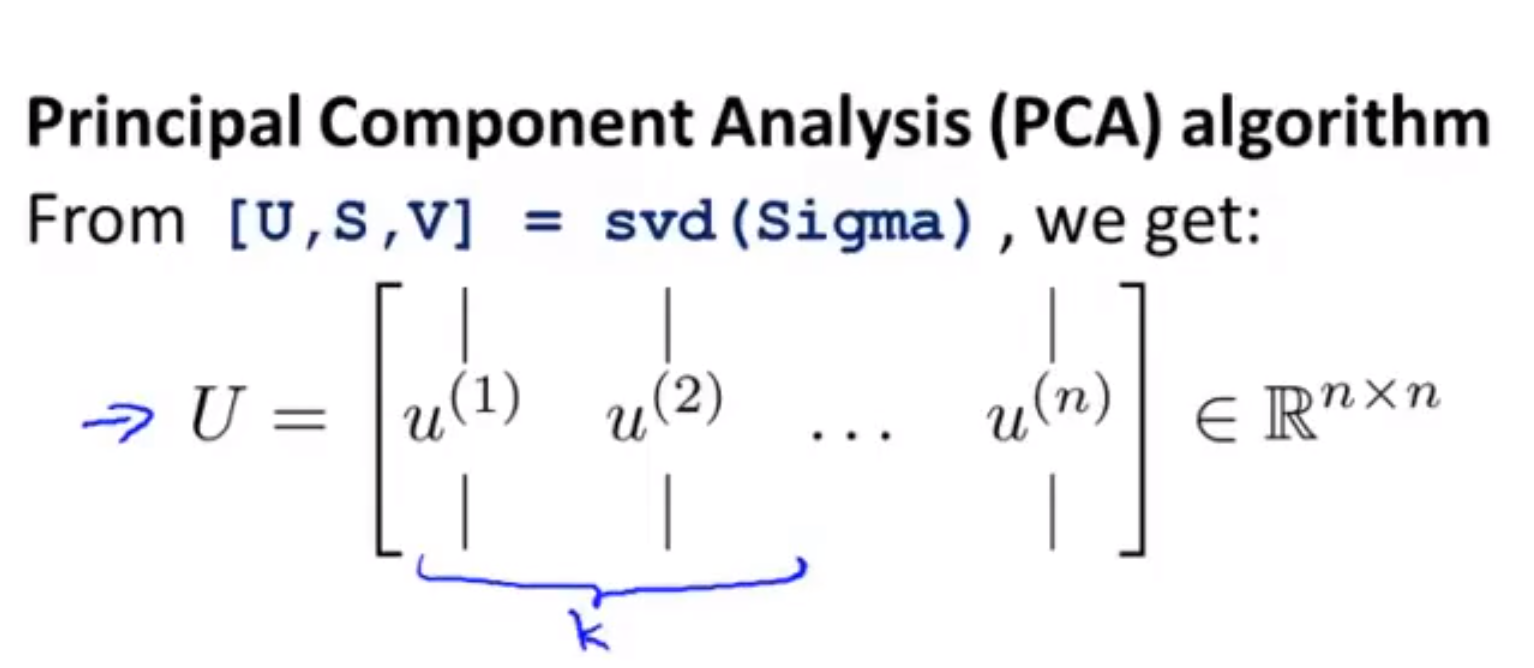
得到的矩阵我们称为U_reduce矩阵,它是一个n*k的矩阵
然后,我们再做运算(Z = U\_reduce^T * X),得到最终结果 , 即 k * m的向量
至此,将n*m矩阵 X 降维到了 k*m 矩阵Z
对于单个样本(n*1)列向量,也可以使用PCA
压缩重现
如果在应用PCA时,如果点到投影面的距离不大,则重构误差较小,此时
[X_{approx} = U_{reduce}*Z \
因为 Z = U_{reduce}^T * X
]
如何选择k值
优化目标: 最小化重构误差
[J = frac{1}{m}sum_{i=1}^m ||x^{(i)}-x^{(i)}_{approx}||^2
]
一个准则: 在满足下列表达式的情况下,所选的k可以尽量小