contest1345
2020-05-09
A.Puzzle Pieces
可见 只有1*n 或者n*1 或者 2*2 的拼图有可能实现 判断即可
A.Puzzle Pieces
可见 只有1*n 或者n*1 或者 2*2 的拼图有可能实现 判断即可
B.Card Constructions
假设有n层,所需要的牌数为
t(n) = ( 3n+1)n/2
假设有n层,所需要的牌数为
t(n) = ( 3n+1)n/2
因此 若有t张牌 则所能构造的最高层数为
1 int cnt = floor(((sqrt((long double)(1 + 24 * k)) - 1)) / 6.0); 2 //oj无法识别某些强制转换语法,所以long double需要打上括号 大概
C. Hilbert's Hotel
我们可以将整个整数域任意分割为无数组长度为n的集合。那么只要一组集合中,每个元素进行变换后,还能够在另外一个集合(即使不是同一个集合)中不重复,即为成功。于是我们可以取0到n-1为初始集合,计算他们变换后占另一个集合的id。
另外对任意一个操作数,加上n也不会改变所占另一集合的id,因此我们先将操作数改为整数,在进行变换。
for int i = 0; i < n; i++) { if (dataa[i] < 0) dataa[i] += ((-1 * dataa[i]) / n + 1) * n;//对负数进行处理 dataa[i] = (i + dataa[i]) % n; //计算操作后的id if (exist[dataa[i]]) { //判断重复 flag = 0; break; } exist[dataa[i]] = 1; } if (flag) cout << "YES "; else cout << "NO ";
D. Monopole Magnets
首先判断不能构成成立的情况
1.N不能走到白格子上,意味这每行每列上,黑格子必须连续,形如
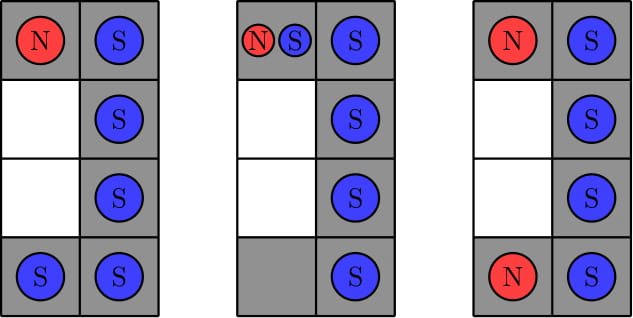
的 都不满足条件
2.每行每列都要有S,说明倘若只有全白行或者全白列时,S无处可放,不成立。但是如果既有全白行也有全白列,S可以放在交点处,就不会影响N的运动。
1.N不能走到白格子上,意味这每行每列上,黑格子必须连续,形如

的 都不满足条件
2.每行每列都要有S,说明倘若只有全白行或者全白列时,S无处可放,不成立。但是如果既有全白行也有全白列,S可以放在交点处,就不会影响N的运动。
然后dfs求连通黑块即可
E. Quantifier Question
题目大意:首先介绍 数学中∀和∃的概念,之后给定m个变量和n次输入
每次输入两个数a,b 有xa<xb
问该如何规定x1到xi的逻辑(例如 ∃x2,∀x1有x1<x2)使所有输入成立,且使∀逻辑尽可能多。(这题写不来)
首先依据给定的大小关系建图。倘若建出的图存在圈,则会导致 **xi<xi** 的现象,为非法,因此我们首先用dfs判断是否存在圈,有则直接输出-1。
判断之后的图必定是个DAG,于是我们继续快乐dfs(
首先要明确在给定xi的逻辑符号为∀时,任何和xi存在可比关系的变量都应为 ∃,而当我们访问了一个已经被标记为∃的点时,我们对其不做处理。
因此我们只要建立正图和反图,进行dfs即可。
题目大意:首先介绍 数学中∀和∃的概念,之后给定m个变量和n次输入
每次输入两个数a,b 有xa<xb
问该如何规定x1到xi的逻辑(例如 ∃x2,∀x1有x1<x2)使所有输入成立,且使∀逻辑尽可能多。(这题写不来)
首先依据给定的大小关系建图。倘若建出的图存在圈,则会导致 **xi<xi** 的现象,为非法,因此我们首先用dfs判断是否存在圈,有则直接输出-1。
判断之后的图必定是个DAG,于是我们继续快乐dfs(
首先要明确在给定xi的逻辑符号为∀时,任何和xi存在可比关系的变量都应为 ∃,而当我们访问了一个已经被标记为∃的点时,我们对其不做处理。
因此我们只要建立正图和反图,进行dfs即可。