引子:
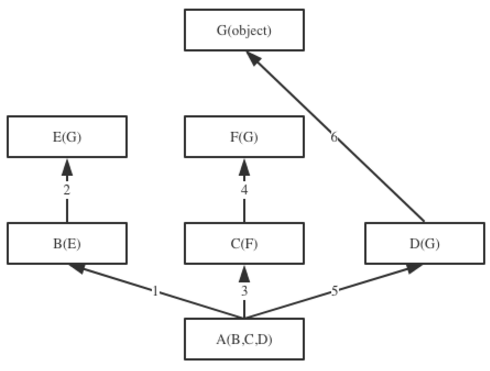
如图反映了python3中,几个类的继承关系和查找顺序。对于类A,其查找顺序为:A,B,E,C,F,D,G,(Object),这并不是一个简单的深度优先或广度优先的规律。那么这个顺序到底是如何产生的?
C3线性是用于获取多重继承下继承顺序的一种算法。通常,被称为方法解析顺序,即MRO(method resolution order)。
算法的名字“C3”并不是缩写,而是指该算法的三大重要属性:
1.前趋图。作为有向无环图,找不到任何的循环,通常用前趋图来理解程序的依赖关系。
2.保持局部的优先次序。
3.单调性。
C3是1996年首次被提出。在python2.3及后续版本中,C3被选定为默认的解析算法。
一个类的C3线性表,是由两部分进行merge操作得到的,第一部分是是它所有父类的C3线性表(parents' linearizations),第二部分是它所有父类组成的列表(parents list)。后者其实是局部的优先级列表。
所谓merge操作,遵循以下原则:表的首个元素不可以出现在其他地方,如果出现了这样的情形,那么就要将该元素全部移出,放到产出列表(output list)中。如果循环进行这一操作,就可以把所有的表逐步移出,逐步扩张产出表,最后得到一个纯粹的产出表。这个产出表就是最后的C3线性表。
举个例子:
python3代码:
class O:
pass
class A(O):
pass
class B(O):
pass
class C(O):
pass
class D(O):
pass
class E(O):
pass
class K1(A, B, C):
pass
class K2(D, B, E):
pass
class K3(D, A):
pass
class Z(K1, K2, K3):
pass
即:
O从以下类继承:无(实际上python3中默认为object类,因为所有类继承于object类,所以才有多种多样的内置方法可用)
A从以下类继承:O
B从以下类继承:O
C从以下类继承:O
D从以下类继承:O
E从以下类继承:O
K1从以下类继承:A,B,C
K2从以下类继承:D,B,E
K3从以下类继承:D,A
Z从以下类继承:K1,K2,K3
为方便起见,记类cls的线性表为L[cls]。
首先,从最简单的类O开始:
L[O]:平凡的情形,直接定为列表[O],即线性表的第一项是自身。所以,L[0]=[O]
L[A]:类A的所有父类是O,所以前一部分是L[O],后一部分是类A所有父类列表[O],前面已经得出L[O]=[O],因此L[A] = [A] + merge(L[O] + [O]) = [A]+merge([O] + [O]) = [A] + [O] = [A,O]
同理:
L[B]=[B,O]
L[C]=[C,O]
L[D]=[D,O]
L[E]=[E,O]
L[K1]:线性表第一项为自身K1,以后的项为其所有父类C3线性表和其所有父类列表的并——
K1继承于A,B,C,所以所有父类C3线性表为:L[A],L[B],L[C];所有父类列表为:A,B,C。
并起来就是merge(L[A],L[B],L[C],A,B,C),然后,遵循原则一步步将其拆开。
L[K1]=[K1]+merge(L[A],L[B],L[C],[A,B,C])
=[K1]+merge([A,O],[B,O],[C,O],[A,B,C])——元素A只在这些列表的首项出现(如:[A,O]和[A,B,C]),应当把它移除到产出列表(output list)。
=[K1,A]+merge([O],[B,O],[C,O],[B,C])——元素O在列表的首项出现过(如:[O]),也在有些列表的剩余项出现过(如[B,O],[C,O]),所以保留它。但是,元素B只在这些列表的首项出现(如:[B,O],[B,C]),应当移出它。
=[K1,A,B]+merge([O],[O],[C,O],[C])——移出B后,同理发现C也是要移出的
=[K1,A,B,C]+merge([O],[O],[O])——merge操作已经走到尽头了
=[K1,A,B,C,O]
L[K2]:K2继承于D,B,E,所以所有父类C3线性表为L[D],L[B],L[E],所有父类列表为D,B,E。同理可得:
L[K2]=[K2]+merge([D,O],[B,O],[C,O],[D,B,E])
=[K2,D]+merge([O],[B,O],[C,O],[B,E])
=[K2,D,B]+merge([O],[O],[C,O],[E])
=[K2,D,B,E]+merge([O],[O],[O],[O])
=[K2,D,B,E,O]
L[K3]:K3继承于D,A,所以所有父类的C3线性表为L[D],L[A],所有父类列表为D,A。同理可得:
L[K3]=[K3,D,A,O]
L[Z]:Z继承于K1,K2,K3。前面计算了K1,K2,K3的线性表,所以这里直接代入计算:
L[Z]=[Z]+merge(L[K1],L[K2],L[K3],K1,K2,K3)
=[Z]+merge([K1,A,B,C,O] , [K2,D,B,E,O] , [K3,D,A,O] , [K1,K2,K3])——应移出K1
=[Z,K1]+merge([A,B,C,O],[K2,D,B,E,O],[K3,D,A,O],[K2,K3])——应移出K2
=[Z,K1,K2]+merge([A,B,C,O],[D,B,E,O],[K3,D,A,O],[K3])——应移出K3
=[Z,K1,K2,K3]+merge([A,B,C,O],[D,B,E,O],[D,A,O])——应移出D
=[Z,K1,K2,K3,D]+merge([A,B,C,O],[B,E,O],[A,O])——应移出A
=[Z,K1,K2,K3,D,A]+merge([B,C,O],[B,E,O],[O])——应移出B
=[Z,K1,K2,K3,D,A,B]+merge([C,O],[E,O],[O])——应移出C
=[Z,K1,K2,K3,D,A,B,C]+merge([O],[E,O],[O])——应移出E
=[Z,K1,K2,K3,D,A,B,C,E]+merge([O],[O],[O])——耗尽,结束
=[Z,K1,K2,K3,D,A,B,C,E,O]
在python3中使用对类help()函数,可以很方便地查看MRO:
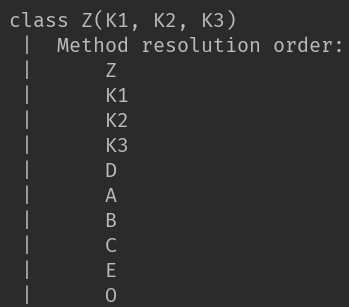
可以看出,python3中的MRO计算,不能以简单地找完一层再找上一层。假如以“广度优先、从左到右、绝不重复”这一规律概括,很容易误认为按照如下顺序查找:
Z从K1,K2,K3继承,所以前三项为K1,K2,K3。接下来找K1的父类A,B,C。再找K2的父类D,B,E,再找K3的父类D,A。但是这样就造成重复。为防止重复,还得定义其他规范。
最后,利用python实现mro的生成。代码可用,但是用了递推函数,有机会以生成器的方式优化防止栈溢出。
1 def not_in_tail(t, L):
2 # 判断一个元素是不是在一个列表的尾巴中出现过。如果从未出现,返回真。
3 if not L:
4 return True
5 if len(L) == 1:
6 return True
7 if t in L[1:]:
8 return False
9 else:
10 return True
11
12
13 def mro(cls):
14 # 如果一个类没有任何父类,那么它的线性表里只有它自己。其实这个类就是object
15 if not cls.__bases__:
16 return [cls, ]
17 # 如果一个类只有一个父类object,那么它的线性表里是先找它自己,再找object
18 if cls.__bases__ == (object,):
19 return [cls, object]
20 # output用于产出线性表,第一项肯定是该类自己。
21 output = [cls, ]
22 # 这里使用递归方法,拿到它所有父类的线性表。后一项为所有父类的列表。
23 merge = [mro(parent) for parent in cls.__bases__] + [list(cls.__bases__), ]
24 while True:
25 # merge操作过程中会不断地把元素取出,可能会有子列表被取空,这时候应直接删除
26 while [] in merge:
27 merge.remove([])
28 # merge操作的终极目标,就是全部剩下object,这就是while的终止条件
29 if all([t == [object, ] for t in merge]):
30 merge = [object, ]
31 break
32 # 准备将欲取出的元素放在head中。该行是一个变量初始化。
33 head = None
34 # 遍历所有的子列表,同时还要拿到索引。
35 for index, sublist in enumerate(merge):
36 # 如果当前子列表只有object,那么就跳过
37 if sublist == [object, ]:
38 continue
39 # 判断子列表的第一项是否满足条件:从未在任何列表的尾巴中出现。如果满足此条件,记下此元素,退出循环准备删除
40 if all([not_in_tail(sublist[0], l) for l in merge[index:]]):
41 head = sublist[0]
42 break
43 if head:
44 # 将该元素添加到线性表中
45 output.append(head)
46 # 将该元素从所有子列表中删除
47 for l in merge:
48 if head in l:
49 l.remove(head)
50 # 从最终返回的列表可以看出产生线性表的两部分结构。merge的终极目标就是只剩下[object,],补上即可
51 mro_list = output + [object, ]
52 return mro_list
53
54 # 以下是测试用例
55 class O:
56 pass
57
58
59 class A(O):
60 pass
61
62
63 class B(O):
64 pass
65
66
67 class C(O):
68 pass
69
70
71 class D(O):
72 pass
73
74
75 class E(O):
76 pass
77
78
79 class K1(A, B, C):
80 pass
81
82
83 class K2(D, B, E):
84 pass
85
86
87 class K3(D, A):
88 pass
89
90
91 class Z(K1, K2, K3):
92 pass
93
94
95 print(mro(Z))
96
97 print(mro(O))
输出结果为:
1 [<class '__main__.Z'>, <class '__main__.K1'>, <class '__main__.K2'>, <class '__main__.K3'>, <class '__main__.D'>, <class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.E'>, <class '__main__.O'>, <class 'object'>]
2
3 [<class '__main__.O'>, <class 'object'>]
可以通过__mro__方法验证:
1 print(Z.__mro__)
2
3 (<class '__main__.Z'>, <class '__main__.K1'>, <class '__main__.K2'>, <class '__main__.K3'>, <class '__main__.D'>, <class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.E'>, <class '__main__.O'>, <class 'object'>)
当然,__mro__方法返回的是元组。所以前面的python代码可以利用tuple()改成以元组形式返回。在递推时,加一层list()以元组形式传入。不再展开。
回到开头的引子。经过验证,答案完全正确:
class G:pass class E(G):pass class B(E):pass class F(G):pass class C(F):pass class D(G):pass class A(B,C,D):pass print(mro(A)) print(A.__mro__) [<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.F'>, <class '__main__.D'>, <class '__main__.G'>, <class 'object'>] (<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.F'>, <class '__main__.D'>, <class '__main__.G'>, <class 'object'>)