Problem B. 即时战略 (rts.c/cpp/pas)
注意
Input file: rts.in
Output file: rts.out
Time Limit : 2 seconds
Memory Limit: 512 megabytes
题面
( ext{HLY})在玩一个即时战略( ext{(Real Time Strategy)})游戏。与大多数同类游戏类似,这个游戏的地图是平面的,并且玩家都有一个基地。
( ext{HLY})的对手杰哥的基地是一个(w imes h)的矩形。其中矩形的每个格子都有一个建筑,每个建筑都有一个重要度。其中第(i)行第(j)列的格子中的建筑的重要度为(w_{ij})。
( ext{HLY})决定轰炸杰哥的基地。他可以选择杰哥基地的任何一个格子释放一个能量为(p)的炸弹。释放以后,这个格子的建筑会受到(p)的摧毁度。炸弹产生的冲击波可以向四个方向扩散,每扩散一格能量值会减少(1)。即释放位置相邻的(4)个格子会受到(p − 1)的摧毁度,再向外的(8)个格子会受到(p − 2)的摧毁度 ... 直到能量值减为 (0) ,形式化的讲,如果在第 (x) 行第 (y) 列释放炸弹,那么第 (i) 行第$ j$ 列的格子受到的摧毁度 $d_{ij} = max(0,p − (| x − i | + | y − j |)) $。
对于每个的格子,杰哥受到的损失即为这个格子的重要度与受到的摧毁度的乘积,即(w_{ij} imes d_{ij})。
( ext{HLY})想知道,对于每一种投放炸弹的方案,杰哥受到的最小总损失和最大总损失各为多少,形式化的讲,即为
的最小值与最大值。
输入格式
第(1)行三个整数(w,h,p)。
接下来(w)行,每行(h)个整数。从第(2)行开始第(i)行第(j)个整数表示(w_{ij})。
输出格式
一行两个数,表示杰哥受到的最小总损失和最大总损失,用空格隔开。
样例
( exttt{input#1})
3 4 3
9 9 9 1
9 9 1 1
9 1 1 1
( exttt{output#1})
10 96
数据范围与提示
样例解释:
( ext{HLY})在第(2)行第(2)列释放炸弹杰哥所受损失最大,为
(9 imes 1 + 9 imes 2 + 9 imes 1 + 9 imes 2 + 9 imes 3 + 1 imes 2 + 1 imes 1 + 9 imes 1 + 1 imes 2 + 1 imes 1 = 96)。
( ext{HLY})在第(3)行第(4)列释放炸弹杰哥所受损失最小, 为
(1 imes1+1 imes1+1 imes2+1 imes1+1 imes2+1 imes3 = 10)。
对于(100%)的数据,(1 le n,m le 400,1 le p le 200,0 le w ij le 10^5)。
子任务(1)((10)分) :满足(p= 1)。
子任务(2)((30)分) :满足(1 le n,m le 40)。
子任务(3)((60)分) :没有特殊限制。
题解
(1 le n,m le 400)模拟可过,不过需要点技巧——前缀和。
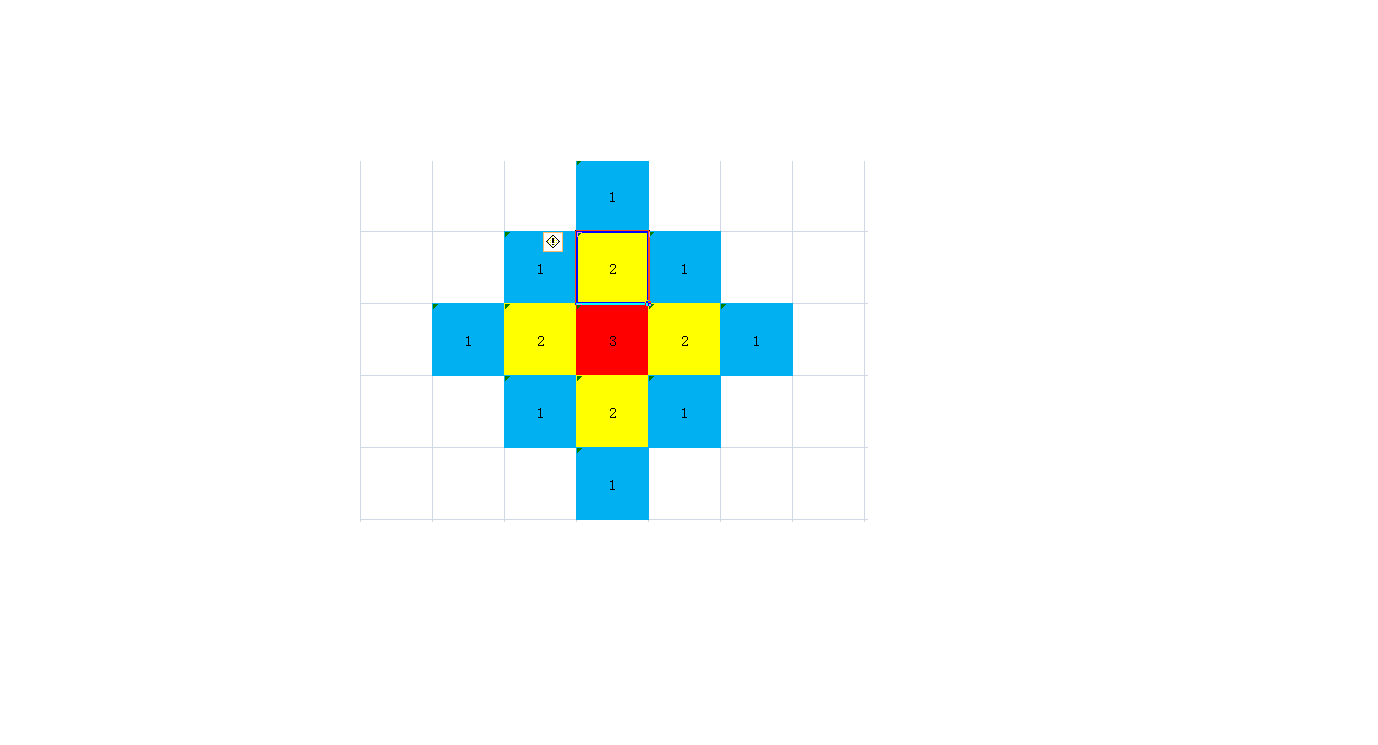
一个能量为(3)的炸弹产生的影响如上图。
很明显是(3)个菱形,我们计算每个菱形的边加到一起。
但暴力加明显过不了,所以使用前缀和,维护一个从左上到右下的前缀和以及一个从右上到坐下的前缀和(是一条线上的)。
具体看代码。
(Code)
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#define max(a,b) a>b?a:b
#define min(a,b) a<b?a:b
#define MAXN 2020
#define int long long
int w,h,p,ans1=0,ans2=1e18,map[MAXN][MAXN];
int sum1[MAXN][MAXN],sum2[MAXN][MAXN];
inline void read(int &T) {
int x=0;bool f=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=!f;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
T=f?-x:x;
}
signed main() {
read(w),read(h),read(p);
w+=500,h+=500;//防止越界
for(int i=501;i<=w;++i) {
for(int j=501;j<=h;++j) {
read(map[i][j]);
}
}
for(int i=1;i<=2010;++i) {
for(int j=1;j<=2010;++j) {
sum1[i][j]=sum1[i-1][j-1]+map[i][j];
}
}//一个从左上到右下的前缀和
for(int i=1;i<=2010;++i) {
for(int j=2010;j>=1;--j) {
sum2[i][j]=sum2[i-1][j+1]+map[i][j];
}
}//一个从右上到左下的前缀和
for(int i=501;i<=w;++i) {
for(int j=501;j<=h;++j) {//枚举将炸弹放到哪一个点
int sum=p*map[i][j];
int x=p;
while(x>1) {
sum+=(p-x+1)*(sum1[i][j+x-1]-sum1[i-x][j-1]);
sum+=(p-x+1)*(sum1[i+x-1][j]-sum1[i-1][j-x]);
sum+=(p-x+1)*(sum2[i][j-x+1]-sum2[i-x][j+1]);
sum+=(p-x+1)*(sum2[i+x-1][j]-sum2[i-1][j+x]);
sum-=(p-x+1)*map[i-x+1][j];
sum-=(p-x+1)*map[i+x-1][j];
sum-=(p-x+1)*map[i][j-x+1];
sum-=(p-x+1)*map[i][j+x-1];
--x;
}//计算放到该点的摧毁度
ans1=max(ans1,sum);
ans2=min(ans2,sum);
}
}
std::cout<<ans2<<" "<<ans1<<'
';
return 0;
}