二分查找
P1024 一元三次方程求解
题目给出范围[-100,100],同时两根绝对值之差<=1,保证了每一个大小为1的区间里至多有1个解,也就是说当区间的两个端点的函数值异号时区间内一定有一个解,同号时一定没有解。
也就可以二分去做查找。
AC码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; double a,b,c,d; double f(double x) { return a*x*x*x+b*x*x+c*x+d; } int main() { double l,r,x1,x2,mid; int cnt=0; scanf("%lf%lf%lf%lf",&a,&b,&c,&d); for(int i=-100;i<=100;i++) { l=i; r=i+1; x1=f(l); x2=f(r); if(!x1) { printf("%.2lf ",l); cnt++; } if(x1*x2<0) { while((r-l)>=0.001) { mid=(l+r)/2; if(f(mid)*f(r)<=0) { l=mid; } else r=mid; } printf("%.2lf ",r); cnt++; } if(cnt==3) break; } return 0; }
这里对以下的一段代码稍稍说明一下
while((r-l)>=0.001)//区间左右距离在可行的范围内 { mid=(l+r)/2;//中间值,也就是二分点 if(f(mid)*f(r)<=0)//判断条件(根据题意可以进行替换) { l=mid;//接着查找右区间[mid,r] } else r=mid;//接着查找左区间[l,mid] }
上面就是二分的核心部分,至于判断条件,根据题意自己写个·bool函数吧
P1182 数列分段 Section II
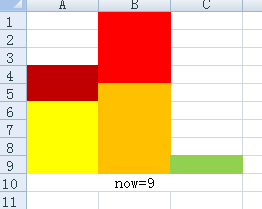
首先画一条线,也就是分段后和的最大值(一般去mid),也就是这里的now。
然后逐渐减小这个now,只要分段数(cnt)合法。
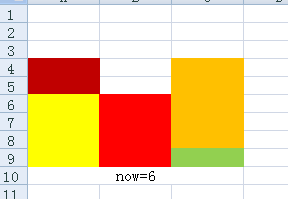
第二次:now=6,cnt=3.
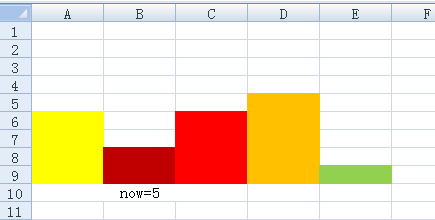
第三次:now=5,但是cnt=4(不合法),结束。
AC码:
#include<cstdio> #include<cstring> #define maxn 100010 #include<algorithm> using namespace std; int n,m,a[maxn],now,cnt; bool pd(int mid) { now=mid;cnt=1; for(int i=1;i<=n;i++) { if(now<a[i]) { cnt++; now=mid-a[i]; } else now-=a[i]; } return cnt<=m; } int main() { int l=0,r=0; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); l=max(l,a[i]); r+=a[i]; } int mid; while(l<r) { mid=(l+r)>>1; if(pd(mid)) r=mid; else l=mid+1; } printf("%d",l); return 0; }
P2678 跳石头
二分跳跃距离,然后把这个跳跃距离“认为”是最短的跳跃距离,然后去以这个距离为标准移石头。判断这个解是不是可行解。如果这个解是可行解,那么有可能会有比这更优的解,那么我们就去它的右边二分。为什么去右边?答案是,这个区间是递增的 ,而我们求的是最短跳跃距离的最大值,显然再右边的值肯定比左边大,那么我们就有可能找到比这更优的解,直到找不到,那么最后找到的解就有理由认为是区间内最优解。反过来,如果二分到的这个解是一个非法解,我们就不可能再去右边找了。因为性质,右边的解一定全都是非法解。那么我们就应该去左边找解。
如何实现判断呢?可以去模拟这个跳石头的过程。开始你在i(i=0)位置,我在跳下一步的时候去判断我这个当前跳跃的距离,如果这个跳跃距离比二分出来的mid小,那这就是一个不合法的石头,应该移走。为什么?我们二分的是最短跳跃距离,已经是最短了,如果跳跃距离比最短更短岂不是显然不合法,是这样的吧。移走之后要怎么做?先把计数器加上1,再考虑向前跳啊。去看移走之后的下一块石头,再次判断跳过去的距离,如果这次的跳跃距离比最短的长,那么这样跳是完全可以的,我们就跳过去,继续判断,如果跳过去的距离不合法就再拿走,这样不断进行这个操作,直到i = n+1,为啥是n+1?河中间有n块石头,显然终点在n+1处。(这里千万要注意不要把n认为是终点,实际上从n还要跳一步才能到终点)。模拟完这个过程,我们查看计数器的值,这个值代表的含义是我们以mid作为答案需要移走的石头数量,然后判断这个数量 是不是超了就行。如果超了就返回false,不超就返回true。
AC码:
#include<cstdio> #include<cstring> #define maxn 500010 #include<algorithm> using namespace std; int l,r,n,m,a[maxn],d,ans; bool pd(int mid) { int tot=0,next=0,now=0;//next下个石头、now当前所在石头 while(next<n+1) { next++; if(a[next]-a[now]<mid) { tot++;//拿走石头,再看下一块 } else now=next;//不拿,直接跳过去 } if(tot>m) return false; else return true; } int main() { scanf("%d%d%d",&d,&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } a[n+1]=d;//n+1,注意 l=1;r=d; int mid; while(l<=r) { mid=(l+r)>>1; if(pd(mid)) { ans=mid; l=mid+1; } else r=mid-1; } printf("%d",ans); return 0; }
P2985 [USACO10FEB]吃巧克力Chocolate Eating
先二分求出最不开心那天的最大开心值ans
再对ans重新走一遍以记录正确日期(这里大概最难吧)
直接代码
#include<cstdio> #include<cstring> #include<algorithm> #define maxn 500010 using namespace std; long long ans,day[maxn],l,r,mid,n,d,h[maxn]; bool eat(long long x) { long long cnt=0,sum=0; for(int i=1;i<=d;i++) { sum=sum>>1; while(sum<x) { sum+=h[++cnt];//达不到x便返回 if(cnt>n) return false; if(x&&x==ans) day[cnt]=i;//if保证仅对ans记录日期 } } return true; } int main() { scanf("%lld%lld",&n,&d); for(int i=1;i<=n;i++) { scanf("%lld",&h[i]); r+=h[i]; } while(l<=r) { mid=(l+r)>>1; if(eat(mid)) { ans=mid; l=mid+1; } else r=mid-1; } printf("%lld ",ans); eat(ans); for(int i=1;i<=n;i++) { if(day[i]) printf("%lld ",day[i]); else printf("%lld ",d);//要吃完巧克力,剩下的就直接输出没吃的 } return 0; }
P1314 聪明的质监员(要被开除的质检员)
在W取0时,所有的区间内的矿石都可以选上,
而在W大于最大的质量时,所有的矿石都选不上。
然后简单算一下就发现:
W越大,矿石选的越少,W越小,矿石选的越多。
所以w↑,y↓
当Y>s 时,需要增大WW来减小YY,从而|Y-s|变小;
当Y==s时,∣Y−s∣==0;
当Y<s时,需要减小W来增大YY,从而|Y-s|变大;
之后用前缀和去算区间val和,这样快。
AC码:
#include<cstdio> #include<cstring> #include<algorithm> #define maxn 200010 #define ll long long using namespace std; ll ans,s; int n,m,w[maxn],v[maxn],l[maxn],r[maxn],maxx,minn=2147483647; ll qaqn[maxn],qaqv[maxn],tot,sum; bool pd(int ww) { tot=0,sum=0; memset(qaqn,0,sizeof(qaqn)); memset(qaqv,0,sizeof(qaqv)); for(int i=1;i<=n;i++) { if(w[i]>=ww) { qaqn[i]=qaqn[i-1]+1; qaqv[i]=qaqv[i-1]+v[i]; } else { qaqn[i]=qaqn[i-1]; qaqv[i]=qaqv[i-1]; } } for(int i=1;i<=m;i++) { tot+=(qaqn[r[i]]-qaqn[l[i]-1])*(qaqv[r[i]]-qaqv[l[i]-1]); } sum+=llabs(tot-s); if(tot>s) return true; else return false; } int main() { scanf("%d%d%lld",&n,&m,&s); for(int i=1;i<=n;i++) { scanf("%d%d",&w[i],&v[i]); maxx=max(maxx,w[i]); minn=min(minn,w[i]); } for(int i=1;i<=m;i++) { scanf("%d%d",&l[i],&r[i]); } int ql=minn-1,qr=maxx+2,mid; ll ans=0x3f3f3f3f3f3f3f3f; while(ql<=qr) { mid=(ql+qr)>>1; if(pd(mid)) ql=mid+1; else qr=mid-1; ans=min(sum,ans); } printf("%lld",ans); return 0; }
P2571 [SCOI2010]传送带
三分套三分,把线段ab三分寻找转折点后从转折点跑向线段cd,然后再在线段cd上三分寻找抵达地点跑向点d。
之后我陷入了一脸懵的状态,三分与a,c的距离,但是这个距离根本无法确定该点的坐标。
之后看了大佬的题解后...啥!还可以三分比例!
然后

不是太理解。。。讲不出来,只好把那位dalao的话引用过来了
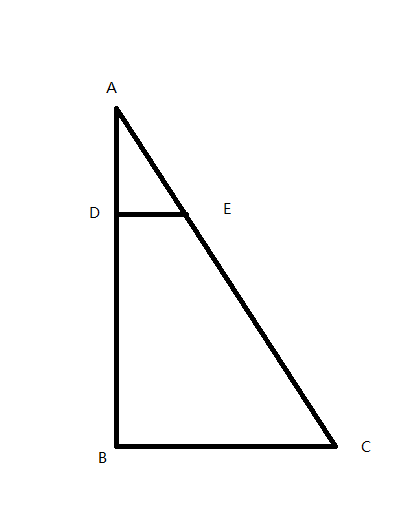
我们现在已知线段AC,假设现在在AC上已找到一点E,我们要去计算E与另一条线段的距离,这个E的坐标怎么求呢?
以AC为斜边,作一个Rt△ABC。作ED⊥CB,此时我们可以发现,△AED和△ACB是相似三角形
所以AE和AC有一定的比值,即AC/AE=k(0≤k≤1)。
所以我们可以直接三分k,然后就可以求出F的坐标了。
AC码:
#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define maxn 10010 #define eps 1e-7 using namespace std; double ax,ay,bx,by,cx,cy,dx,dy,P,Q,R;//其实可以用结构体来存四个点的坐标,这样后面的函数更方便写 double dis(double x,double y,double xx,double yy)//又臭又长 { return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy)); } double ctx(double x,double xx,double k) { double qaq; qaq=(xx-x)*k+x; return qaq; } double cty(double y,double yy,double k) { double qwq; qwq=(yy-y)*k+y; return qwq; } double expd(double x,double y) { double nx1=ctx(ax,bx,x),ny1=cty(ay,by,x),nx2=ctx(cx,dx,y),ny2=cty(cy,dy,y);//这就是不用结构体的下场 return dis(ax,ay,nx1,ny1)/P+dis(nx1,ny1,nx2,ny2)/R+dis(nx2,ny2,dx,dy)/Q; } double pd(double x) { double l=0.0,r=1.0; while(r-l>=eps) { double mid=l+(r-l)/3.0,mmid=r-(r-l)/3.0; if(expd(x,mid)>expd(x,mmid)) l=mid; else r=mmid; } return expd(x,l); } int main() { scanf("%lf%lf%lf%lf",&ax,&ay,&bx,&by); scanf("%lf%lf%lf%lf",&cx,&cy,&dx,&dy); scanf("%lf%lf%lf",&P,&Q,&R); double l=0.0,r=1.0; while(r-l>=eps) { double mid=l+(r-l)/3.0,mmid=r-(r-l)/3.0; if(pd(mid)>pd(mmid)) l=mid; else r=mmid; } printf("%.2lf",pd(l)); return 0; }
2019-08-01 23:42:18