平面上有n个两两没有公共点的圆,i号圆的圆心在(xi,yi),半径为ri,编号从1开始。求所有最外层的,即不包含于其他圆内部的圆。输出符合要求的圆的个数和编号。n<=40000.
(注意此题无相交相切!!!)
工具:扫描线+set
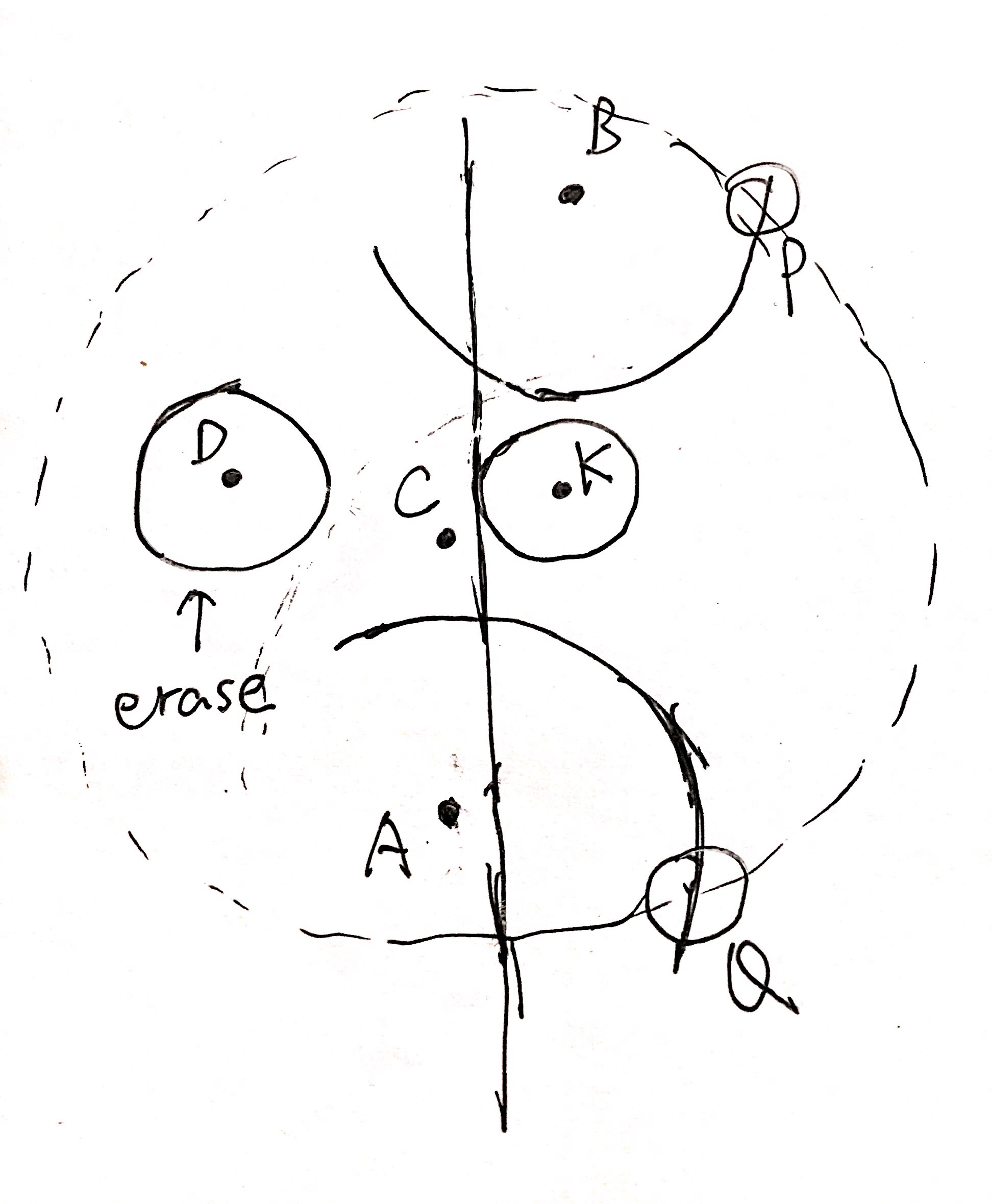
中心思想:
边界分左右端点,如图,当扫描线与k号圆左端点相切,之前用set维护一个y纵坐标的二叉树,那我们在二叉树中查找离k号圆纵坐标最近的上下两个圆(A,B),让k与A,B判是否内含即可,为什么是AB?假设有C点(离k远一些)包含k,但A不包含k,那么一定有A,C相交,这不符合题意。
之后,当扫到右端点,从set中删掉这个圆(即图中的D,因为它对后面k的判断没卵关系,而且还可能阻碍A,B)
上代码:
typedef pair<double,int>P; struct node{ double x,y,r; }nod; bool inside(int a,b){//判断a是否在b中,半径大于圆心距 double dx=node[a].x-node[b].x,dy=node[a].y-node[b].y; return dx*dx+dy*dy-node[b].r*node[b].r<=eps; } void solve(){ vector<P>point; set<P>outer;//记录与当前扫描线相交的最外层圆集合 vector<int>ans;//真正存储最外层圆集合 For(i,1,n){ point.pb(P(nod[i].x-nod[i].r,i));//记录左端点 point.pb(P(nod[i].x+nod[i].r,i+n));//记录右端点 } sort(point+1,point+1+n); For(i,0,point.size()-1){ int id=point[i].sd; if(point[i].sd<n){//扫到左端点 set<P>::iterator it=outer.lower_bound(P(nod[id].y,id));//二分找A,B if(it!=outer.begin()&&inside(id,it->sd))continue; if(it!=outer.end()&&inside(id,(--it)->sd))continue; ans.pb(P(nod[id].y,id)); outer.insert(P(nod[id].y,id)); }else outer.erase(P(node[id].y,id)); //扫到右端点,删掉 } sort(ans.begin(),ans.end());