POJ1127 Jack Straws

给你一些线段，求出哪些线段是相连的，哪些是不相连的。相连包括间接相连，即这两条线段本身不直接相连，而是通过其它线段的连接而间接相连。

线段相交+并查集

这里主要说如何判断线段相交：快速排斥试验+跨立试验
牢记一点：研究对象一定是两条线段的四个端点

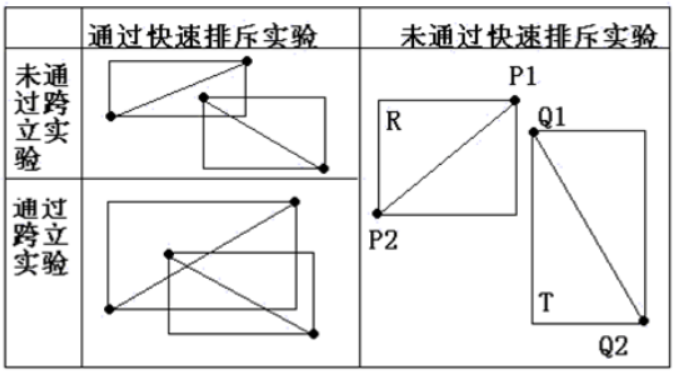
（快速排斥试验：只是可以证明这两条一定不相交，达到一点加速效果）
以线段P1，P2为对角线作一矩形R，再以Q1,Q2为对角线作矩形T，当两个矩形不相交的时候两条线段肯定不相交，即线段相交的必要条件时矩形相交。
矩阵相交依据：两条线段一共四个端点，x/y轴中，最小的两个端点不能属于同一条线段
min(p1.x,p2.x)<=max(q1.x,q2.x)&&
min(q1.x,q2.x)<=max(p1.x,p2.x)&&
min(p1.y,p2.y)<=max(q1.y,q2.y)&&
min(q1.y,q2.y)<=max(p1.y,p2.y)

（跨立试验：叉乘+点乘，保证一条线段的两端点在另一条线段的两侧）
(Q1P1xQ1Q2)*(Q1Q2xQ1P2)>0
(P1Q1xP1P2)*(P1Q2xP1P2)>0
叉乘公式：
a x b=(l,m,n)x(o,p,q)=((mq-pn),(no-lq),(lp-mo))
平面的话 a x b=(a.x,a.y,0)x(b.x,b.y,0)=(0,0,a.x*b.y-a.y-b.x)

上代码：

struct point{
int x,y;
};
struct seg{
point a,b;
}S;

int mul(point p1,p2,p3){
return (p1.x-p2.x)*(p3.y-p2.y)-(p1.y-p2.y)*(p3.x-p2.x);
}

bool insect(point p1,p2,q1,q2){
if(max(p1.x,p2.x)<min(q1.x,q2.x)||max(q1.x,q2.x)<min(p1.x,p2.x)||max((max(p1.y,p2.y)<min(q1.y,q2.y)||max(q1.y,q2.y)<min(p1.y,p2.y))return 0;
if(mul(q1,p1,p2)*mul(p2,p1,q2)<=0&&mul(p1,q2,q1)*mul(q1,q2,p2)<=0)return 1;
return 0;
}

int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
void uone(int a,b){
int t1=find(a),t2=find(b);
if(t1==t2)return;
if(rk[t1]>rk[t2])fa[t2]=t1;
else fa[t1]=t2;
if(rk[t1]==rk[t2])rk[t2]++;
}

For(i,2,n)
For(j,1,i-1)
if(find(i)!=find(j)&&insect(seg[i].a,seg[i].b,seg[j].a,seg[j].b))
uone(i,j);