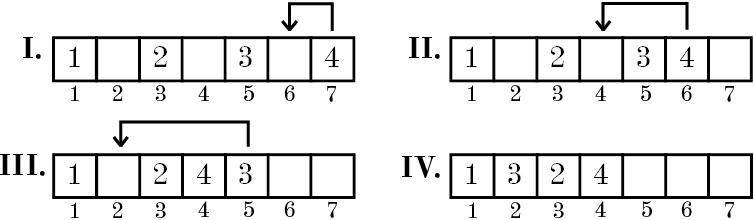
思维题,找规律
1.n为奇数的话,可以用n-1偶数过渡过来(只需要把最后一个丢到最前面)
2.询问的k为奇数的话,直接返回(k+1)/2,因为位置是不改变的
#include <bits/stdc++.h> using namespace std; typedef long long ll; #define inf 2147483647 const ll INF = 0x3f3f3f3f3f3f3f3fll; #define ri register int template <class T> inline T min(T a, T b, T c) { return min(min(a, b), c); } template <class T> inline T max(T a, T b, T c) { return max(max(a, b), c); } template <class T> inline T min(T a, T b, T c, T d) { return min(min(a, b), min(c, d)); } template <class T> inline T max(T a, T b, T c, T d) { return max(max(a, b), max(c, d)); } #define scanf1(x) scanf("%d", &x) #define scanf2(x, y) scanf("%d%d", &x, &y) #define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z) #define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X) #define pi acos(-1) #define me(x, y) memset(x, y, sizeof(x)); #define For(i, a, b) for (int i = a; i <= b; i++) #define FFor(i, a, b) for (int i = a; i >= b; i--) #define bug printf("*********** "); #define mp make_pair #define pb push_back const int maxn = 10005; // name******************************* ll T; ll k, n; ll ans; // function****************************** ll solve(ll n, ll k) { if (n % 2 == 0) { if (k % 2) { return (k + 1) / 2; } else { return solve(n / 2, k / 2) + n / 2; } } else { if (k % 2) { return (k + 1) / 2; } else { if (k == 2) { return solve(n - 1, n - 1) + 1; } else { return solve(n - 1, k - 2) + 1; } } } } //*************************************** int main() { // ios::sync_with_stdio(0); // cin.tie(0); // freopen("test.txt", "r", stdin); // freopen("outout.txt","w",stdout); cin >> n >> T; while (T--) { ans = 0; ll k; cin >> k; cout <<solve(n, k) << endl; } return 0; }