前言
我们知道dom结构也是以树的形式存在的,所以了解树的这种数据结构对于我们分析前端代码还是很重要的。
(当然这里跟前端沾边也是为了吸引大家学习的兴趣,真相其实是我就单纯的想写这一章 ...(。•ˇ‸ˇ•。) ...)
废话不多说,我们先从二叉排序树开始学起吧。
二叉排序树(BST Binary Search Tree)
什么是二叉排序树?
简单来说,就是每一个点只能最多有两个子节点。它有下面三个属性:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树,这点很重要,希望大家记住。
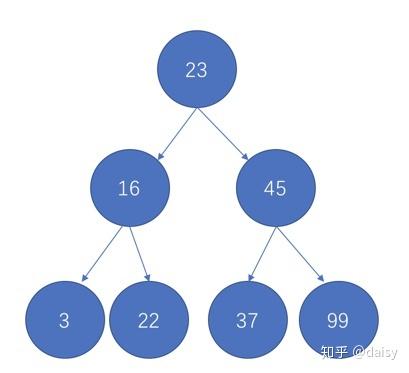
对于这颗树来说,23是它的根节点。而一个父节点的两个子节点分别称为左节点跟右节点。在
二叉树中,左边的节点一定都小于23,右边节点都大于等于23。
实现BST
BST由节点组成。所以先来看看节点的实现:
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = function () {
return this.data;
}
}
这个节点里,传入的data就是节点的数据。left,right分别为左右子节点。
现在需要定义一个二叉查找树(下面简称BST)的类,这个类有一个根节点 root,和一个插入函数insert
function BST() {
this.root = null;
this.insert = insert;
}
难点在于这个插入函数,先抛开这个函数是如何写的,我们先来想想BST是如何长成的。假设我需要在BST里依次插入23,45,16,37,3,99,22这些数字,那么插入的顺序如下:
- 第一个数字为根节点,即 this.root = 23
- 第二个数字为45,对比23,如果比23大,放在23的右边节点。此时BST如下:
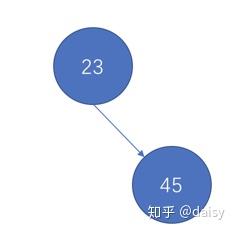
3.第三个数字为16,对比23,比23小,成为23的左节点。此时BST如下:

4.第四个数字为37,先对比23,比23大,放在右边。右边再看23的右节点有值,是45,
37比45小,所以放在45的左边。
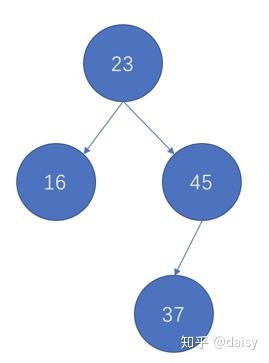
5.第五个数字为3,对比23,比23小,放左边,再看左边23的左节点16,3比16小,
所以放在16的左边。
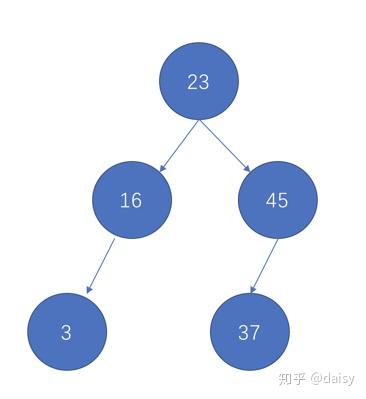
6.第六个数字为99,对比23,比23大,看23的右节点45,比45大,放在45的右节点
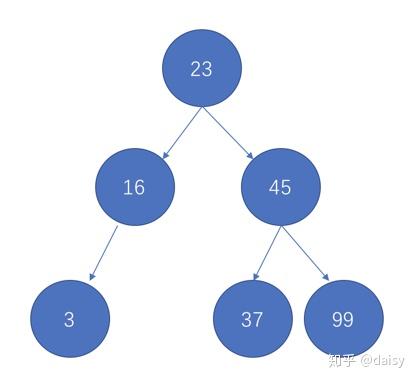
7. 第七个数字为22,对比23,比23小,看23的左节点16,比16大,放在16的右节点。
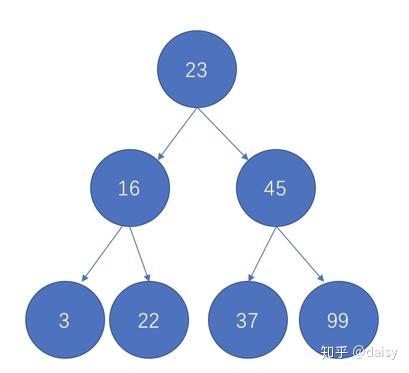
8.如果最后一个数字是100,对比23,比23大,看23的右节点45,比45大,再看45的右节点99,比99大,所以放在99的右节点处。
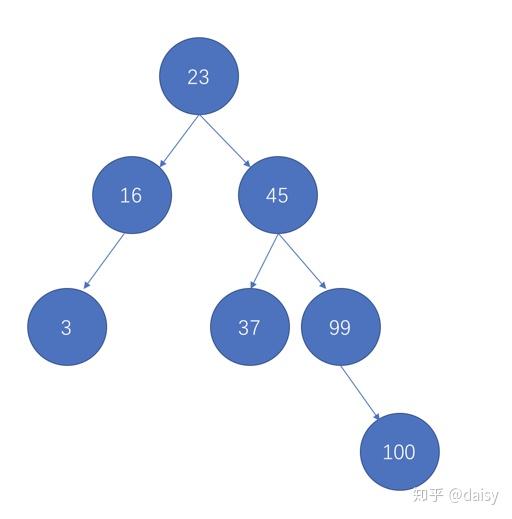
以上,就是一颗BST生成的过程。
接下来我们用计算机的语言描述一下上述过程:(以插入右边节点为例)
- 针对第一个节点,直接将它设置成根节点。
- 设置一个指针parent用于追踪当前的父节点。
- 节点跟当前的parent进行对比,如果 > parent, 看parent.right 是否有值,没有的话,成功找到当前节点n的位置,即parent.right = n,此时终止程序。
- 如果parent.right有值,这么这个parent.right就会成为最新的parent,在重复3步骤。
下面我们用JS来实现一下上述过程:
JS代码实现
function insert(data) {
var n = new Node(data, null, null);
if(!this.root) {
this.root = n;
} else {
// 使用current的指针来探索子节点
var current = this.root;
while(true) {
var parent = current;
if(data < parent.data) {
current = current.left;
if(!current) {
parent.left = n;
break;
}
} else {
current = current.right;
if(!current) {
parent.right = n;
break;
}
}
}
}
}
这样我们这个BST的类就完成啦~~
运行上面的代码:
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(100);
console.log(nums)
在将结果nums打印出来,如果你得到了这样的数据结构,那么恭喜你,你的BST生成成功啦。
( >﹏<。)~

遍历
遍历分为前序,中序,以及后序遍历,他们的命名是以根节点的访问次序划分的:
前序遍历:根节点->左子树->右子树
中序遍历:左子树->根节点->右子树
后序遍历:左子树->右子树->根节点
以我们刚刚生成的BST为例:

前序遍历:23 16 3 22 45 37 99
中序遍历:3 16 22 23 37 45 99 (这时候就会发现:卧槽,6的飞起啊,这不就是升序的排列么)
后序遍历:3 22 16 37 99 45 23
怎么理解呢?以中序遍历为例,由于中序遍历遵循:左子树->根节点->右子树
所以这颗树的排列顺序为 16(左子树) -> 23(根节点) -> 45(右子树)
/ /
3 22 37 99
在看左子树,开篇的时候我们说过,左右字数都依旧是BST,所以对于左右子树,都还是遵循这个排序:左子树->根节点->右子树;
那么,对于左字树来说,排序顺序为3 -> 16 -> 22, 对于右字树,排列顺序是 37 -> 45 -> 99。
连起来就是 3 16 22 23 37 45 99。
前序跟后序同理。