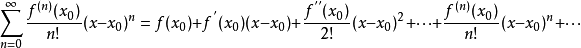嗯,写这个是因为我太弱了(ORZ).
#(mathcal{color{silver}{1 Linear Sieve Method of Prime}})线性筛素数
嗯,其实对于这个而言,无非就是一个(break)不易理解而已。
if(! (i % prime[j])) break ;
那么我们先来分析线性筛的复杂度,嗯,很显然因为是(O(n))才称其为线性筛法。所以也就是说,对于每个合数,我们只让它被筛去一次。那么线性筛是如何保证的呢?答:每个合数都会被自己最小的质因子筛掉。
下面让我们来分析合理性,说是证明其实就是逻辑演绎
证明一:在线性筛法中,每个合数都会被自己最小的质因子筛掉。
我们令(N)为一个合数,且他的标准分解式为$$N = p_1^{k_1}p_2^{k_2}p_3^{k_3}...p_t^{k_t}$$不妨令$$p_1 < p_2 < p_3... <p_t$$ 我们考虑当用(p_1)筛除时,令$$N'=frac{N}{p_1}$$那么会因为(p_i)会第一次被使用而使得(N)被成功筛掉((k_1)的值无关紧要,即无论(N')是否是(i)的倍数,只会在这之后跳出)。但是我们考虑,如果用(p_s (s eq 1))筛除的话,那么若令$$i = frac{N}{p_s}$$,则一定有$$ p_1|i$$从而会使得在(prime[j])刚枚举到(p_1)还未枚举到(p_s)时跳出,使其不能被筛掉。
所以得出结论,在线性筛法中,每个合数都会且仅会被自己最小的质因子筛掉。
证明二:线筛中,每个合数当前不被筛的原因是因为它要被放到之后去筛。
对于(N)的两个因子(p_r < p_s),他们会分别在(i = frac{N}{p_r})和(i' = frac{N}{p_s})时筛掉,因为(p_r< p_s),所以会有(i > i`)。结合证明一,由于(N)一定会被最小的(p_i)筛除,所以可以得出此时的(i)一定为最大,所以必须等到所枚举的(i)更大时,(N)才会被筛除。
#(mathcal{color{gold}{2 Sieve Method of Euler}})欧拉筛
首先我们需要有一个前置技能:(varphi(x) imes phi(y) = varphi(x imes y) <=>(x, y) = 1)
那么类比线性筛而言,我们可以发现,对于一个素数(p)而言,(varphi(p)=p-1),那么因为凡是素数必然在合数之前被筛到,所以我们可以考虑以此为基进行欧拉筛。那么,由于若(W=a imes{b})且(gcd(a,b)=1),就会有(varphi(W)=varphi(a) imes varphi(b)),所以有
else
phi[i*prime[j]]=phi[i]*phi[prime[j]];
那么对于另一种情况(w = i imes j),(i mod j = 0)而言,我们考虑有$$i=j^{n-1} imes {x}$$且其中(gcd(j^n,x)=1)
那么此时就会有$$varphi(w)=varphi(j^n) imes varphi(x)$$
而因为事实上$$varphi(j^{n})=j^n-j^{n-1}$$
故$$varphi(x) imes (j^{n-1}-j^{n-2})=varphi(x) imes varphi(j^{n-1})= varphi(i)$$
所以会有$$varphi(w)=varphi(x) imes j imes(j^{n-1}-j^{n-2})$$
所以:
if(i%prime[j]==0)
{
phi[i*prime[j]]=prime[j]*phi[i];
break;
}
#(mathcal{color{cyan}{3 Linear Recursion of Inverse Element}})线性推逆元
首先来思考逆元是个什么东西:
若 (a imes x equiv 1 (mod b)) ,且 (a) 与 (b) 互质,那么我们就能定义: (x)为(a)在(mod b)的逆元,记为 (a^{-1})
再来思考逆元有个什么鬼用处:
对于 (frac{a}{b} (mod {p})) ,我们就可以求出 (b) 在 $ mod p $下的逆元,然后乘上 (a),再(mod p),即可得出结果。
好的那么我们来看一下这玩意儿怎么线性推(QAQ):
首先我们令(p = k imes i + r,0 < r < i)
然后显然的是
两边同时乘上(i^{-1})和(r^{-1})
移个小项
换个元
于是就华丽丽地结束了(qwq)
inv[1]=1;
for(i = 2; i <= n; i ++)
{
inv[i] = - (p / i) * inv[p % i] ;
inv[i] = (inv[i] % p + p ) % p ;
}
#(mathcal{color{midnightblue}{4 Euler‘s Formula }})欧拉公式
欧拉公式是世界上最美妙的公式 ——苏格拉底【雾
首先让我们来看看这个公式的样子:$$e^{ix} = cosx + isinx$$其中(i)为复数单位:$$i = sqrt{-1}$$
那么它美妙在哪里呢?我们会发现它联系了最重要的无理数之一——(e)、复数域(i)和基本初等函数(sin)、(cos)这些东西,所以被冠以“最优美、最伟大桥梁”、“数学上的天桥”等美称。
但是这远远不是最美妙的,最美妙的是,当你取(x = pi)时,会有$$e^{pi i} + 1 = 0$$还有什么比这更美妙吗?我们通过这个公式,成功地将两个最重要的超越数(pi)和(e)、复数中的“地基”(i)、自然数中最美妙的(0)和(1),在这一个公式中被我们尽收眼底(qwq)!
那么,现在有没有引起你的兴趣?如果有,我们来看证明吧:
首先我们需要前置技能——泰勒展开。
泰勒公式是将一个在(x=x_0)处具有(n)阶导数的函数(f(x))利用关于((x-x_0))的(n)次多项式来逼近函数的方法。
若函数(f(x))在包含(x_0)的某个闭区间([a,b])上具有(n)阶导数,且在开区间((a,b))上具有((n+1))阶导数,则对闭区间([a,b])上任意一点(x),成立下式:
——(baidu)百科
这就是泰勒展开式,正确性证明暂时不会,右边的那个幂级数又叫做泰勒级数,我们可以理解为我们把某些特定的函数展开成了幂级数的形式。
(ps):如果无法理解的话……看高数去吧!【下册即可
好啦,扯这么多其实就是说,我们右边的(sin)、(cos)都是可以被展开……换种方式表示的(qwq).
那么他们展开之后大约是这样子:$$forall x, sinx = sumlimits_{n = 0}^{infty}{frac{(-1)^n}{2n + 1}!x^{2n + 1}}$$ $$forall x, cosx = sumlimits_{n=0}^{infty}{frac{(-1)^n}{2n}!x^{2n}}$$
等式左边$$e^x = sumlimits_{n=0}^{infty}{frac{1}{n!}}$$而我们来看(i)的次幂们$$i^1 = i,i^2 = -1, i^3 = -i, i^4 = 1.....$$那我们的左边可以得到
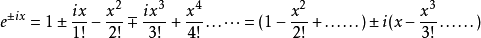
而因为对于(sin)和(cos)的泰勒级数我们可以写成这样:


所以有$$e^{ix} = cosx + isinx$$
证毕。
(ps:)如果你细心+聪明的话,会看到无理数(e)的递推公式哦!
# (color{PINK}{mathcal{5 Number-theory Partitioning}})数论分块
好的,数论分块也叫做整除分块,是数学问题中一个优化时间复杂度的技巧,通常解决的是一个子问题——没错,是用来解决一个很常见的子问题,或者与其相似的子问题。
(233)也就是说大部分情况他就只有一个用处:
求$$sum limits_{i=1}^{n}lfloor frac{n}{i} floor$$并要求复杂度(Theta(sqrt n))
这个问题优化的方向是缩小规模——之所以可以缩小规模,是因为我们发现原来当(n=7) 的时候,(i=5)、(i=6)以及(i=7)的值都一样,于是我们思考可以分块乱搞一下。那么分块怎么分块呢?我们可以有以下这个程序:
for(l = 1 ; l <= N ; l = r + 1){
r = N / (N / l) ;
Ans += (r - l + 1) * (N / l) ;
}
看起来……比较明朗的是这确实是一个分块,并且跟我们上文提及的指导思想十分的相似……
(However)你还是不知道他到底是怎么分的块( m{TAT})
那么精彩的证明就要开始了惹~
(color{red}{Task1})先证一下“指导思想”
这个(emmm)应该是复杂度的证明(233)
命题:$$forall n in N+, i leq n =>cnt(lfloor frac {n}{i} floor) < 2sqrt{n}$$其中(cnt(f(x)))表示整值多项式(f(x))的值域大小。
(人话版本:我们接下来要证明(lfloor frac{n}{i} floor) 最多有(2 sqrt n - 1)种取值,也就是证我们最多要进行的运算次数是(sqrt n)级别的)
以下是证明:
我们分成两种情况来考虑:(i leq sqrt n) 和 (i > sqrt n)
我们先思考简单点的,当(i > sqrt n)时,此时对于全部的(lfloor frac {n}{i} floor)最大不会超过(sqrt n) (- 1),所以其取值不会超过(sqrt n)的级别。
那么对于(i leq n)的情况,我们思考去证明另一件事——证明(lfloor frac {n}{i} floor eq lfloor frac {n}{i + 1} floor)
那么我们此处不妨用反证法,假设(exists lfloor frac {n}{i} floor = lfloor frac {n}{i + 1} floor).我们不妨令(n = i cdot k + q ~ (0 leq q < i)) ,则我们可以得到$$i leq sqrt n leq k$$ 继而得到$$k > q$$
那么根据假设,我们很显然会有$$n = (i + 1) cdot k + q', (0 leq q' < i+1)$$
也就会有下面这个等式$$n = i cdot k + k + q' = i cdot k + q + (k + q' - q) = n + (k + q' - q)$$ 但是因为我们已经证完了的(k > q) 所以等式左边一定不会等于等式右边……所以出现矛盾。
那么我们就通过反证法证明了结论(lfloor frac {n}{i} floor eq lfloor frac {n}{i + 1} floor),从而有几个不同的(i leq n)就会有几个不同的取值。
所以得出结论,(cnt(lfloor frac {n}{i} floor) < 2sqrt n)
好的,刚才的证明和正确性没啥关系……好吧跟时间复杂度的正确性有关系……那就跟正确性有关系好了……我在说些什么奇怪的东西……2333333333333333333
接下来证明那一句玄学的
r = N / (N / l) ;
(color{red}{Task2})再证一下正确性
首先我们意会一下……我们所做的工作,就是要找出极小的(l)和极大的(r),对于给定的(omega)有$ c in [l,r](,)lfloor frac{n}{c} floor = omega$ 。那么根据我们上一个证明中的下半部分我们可以知道,这就是一个极大块,并且下一个极大块是从(r + 1)开始的,因为极大块必然满足(lfloor frac {n}{r} floor eq lfloor frac {n}{r + 1} floor).
那么我们要找的就是每个极大块的右断点(r)。
命题:如果已知(n,p in N+,p leq n),那么满足(lfloor frac {n}{p} floor = lfloor frac {n}{i} floor)的最大的(i)满足$$i = lfloor frac {n}{lfloor frac{n}{p} floor} floor $$
(其实这个玩意儿是可以意会出来的(233))
以下是证明:
我们不妨继续分类讨论:
当(p leq sqrt n)时:
不妨继续设(n = k cdot p + q, (0 leq q < p))
那么我们可以得到比较显然的结论是$$lfloor frac {n}{lfloor frac{n}{p} floor} floor = lfloor frac {n}{k} floor$$且因为当(p leq sqrt n)时,(lfloor frac {n}{p} floor)互不相同,所以(i_{maxp} = p),我们只需要证明 $$p= lfloor frac {n}{k} floor$$ 而这个结论是显然的。因为(q < p leq k) ,所以得证(p = lfloor frac {n}{k} floor)
当(p > sqrt n) 时:
直接证似乎不是很容易,那么我们思考一个转化。因为对于一个(p)我们要证明的(i_{maxp})有两个性质:$$lfloor frac {n}{i_{maxp}} floor = lfloor frac {n}{p} floor = k$$并且$$lfloor frac {n}{i_{maxp} + 1} floor eq lfloor frac {n}{p} floor$$
那么由于$lfloor frac {n}{lfloor frac{n}{p} floor} floor = lfloor frac {n}{k} floor $ 所以我们不妨把要求的(i_{maxp})换成$lfloor frac {n}{k} floor $ 并说明$$lfloor frac {n}{lfloor frac {n}{k} floor} floor = lfloor frac {n}{p} floor = k$$并且 $$lfloor frac {n}{ lfloor frac {n}{k} floor+ 1} floor eq lfloor frac {n}{p} floor$$
而此时由于(k < sqrt n), 所以我们发现原来就是当(p leq sqrt n)时的结论。于是我们就无比迅速地得到了(lfloor frac {n}{lfloor frac {n}{k} floor} floor = k)并且由(Task1)中的结论推出了(lfloor frac {n}{ lfloor frac {n}{k} floor+ 1} floor eq k)。
于是乎:
那么我们就证完了!想不到这个这么显然的结论这么好背的结论居然是迄今为止这篇博客中我花费心血最多的(233)……
嗯,我被自己帅到了嘿嘿~
#(mathcal{color{lavender}{6 ~Something~About~Ackerman~Function}}) 阿克曼函数相关
不知道为什么就开始颓这个函数……
感觉很牛13的样子……
以下大部分内容来自(Wiki)(主要是智障楼主找不到更好的材料了)
首先我们先解释一下箭头表示法这个东西(一时编不出什么更好的名字)
我们用(uparrow)表示“迭代相乘”,譬如说(2uparrow4)表示(2^4),而(3uparrow4)则表示(3^4)。
同时,我们用(uparrow uparrow)表示“迭代取幂”,它的意思是(a uparrow uparrow b = a^{a^{cdot^{ cdot^{ cdot ^a}}}}) ,等式右边一共有(b) 个(a)。
同时,我们用(uparrow uparrow uparrow)表示“迭代迭代取幂”……
好吧,其实这玩意儿是递归定义的,借鉴的(wiki)的我承认(233)……
那么这东西用处是啥呢?其实我们如果用它来表示大数的话,是比科学计数法更容易的,比如(a^{19260817})就看起来很繁琐是吧(233)
那么接下来,我们来介绍真正地(Ackerman)函数。很巧的是,这东西也是递归定义的:
并且,这东西十分的大,当(m geq 4 ~ & ~n > 2)的时候就已经十分不可算了,因为事实上(A(4,3) = 2^{65536} - 3),不知道会不会爆(python~23333)