Description
有长为 $ n$ 的序列 \(a[1...n]\)
按 \(j = (0, 1, 2, ... , n - 1)\) 依次输出把大于 \(j\) 的 \(a[i]\) 改为 \(j\) 后逆序对的个数。
Constraints
\(1 \le n \le 10^6\), \(0 \le \forall a[i] \le n\)。
Solution
平常的逆序对可以直接用树状数组维护,但是这题有多次询问,每次还会对一些数进行“削平”,不能直接处理。
在“削平”中,原数组的一些逆序对会消掉,可以从这里考虑。
设一个逆序对为\([a_x, a_y](a_x > a_y)\),当前 \(j\) 的值为 \(k\), 思考什么时候这个逆序对会存在或消失:
-
当 \(k > a_y\) 时,\(a_x\) 再怎么削也仍比 \(a_y\) 要大,能够存在。
-
当 \(k \le a_y\)时,\(a_x\) 会被削到比 \(a_y\) 小或相等,逆序对消失。
倒过来考虑,所以当 \(j\) 从 \(k - 1\) 增加到 \(k\) 时,满足 \(a_y = k\) 的逆序对会新产生。
所以在此过程答案每次增加量是序列中 \(a_y = k\) 的逆序对个数。
考虑用树状数组维护逆序对,再设 \(cnt[i]\) 数组累加 \(a[i]\) 数值 的逆序对个数。
因为 \(a\) 数组中的数值可能会有相等,而在不同位置相等的数值对答案都会有贡献,应当累加。
每次询问的答案自然是每次增加量之和,即 \(cnt[1] \sim cnt[j - 1]\) 的和(不是到 \(cnt[j]\),原因在上面解释了)。
举个例子助理解:
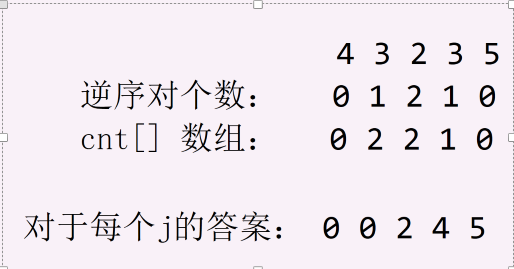
最后还是得注意树状数组不能处理下标为 \(0\) 的位置,所以要给每个 \(a[i]+1\)。
Code
// by youyou2007 in 2022.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#include <map>
#define int long long
#define REP(i, x, y) for(int i = x; i < y; i++)
#define rep(i, x, y) for(int i = x; i <= y; i++)
#define PER(i, x, y) for(int i = x; i > y; i--)
#define per(i, x, y) for(int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
const int N = 1E5 + 5;
int n;
int a[N];
int tree[N];
int cnt[N];
int lowbit(int x)
{
return x & (-x);
}
void add(int x, int y)
{
while(x <= n + 1)//因为 a[i] 都 +1 了,最大范围也要 +1
{
tree[x] += y;
x += lowbit(x);
}
}
int query(int x)
{
int res = 0;
while(x > 0)
{
res += tree[x];
x -= lowbit(x);
}
return res;
}
signed main()
{
scanf("%lld", &n);
rep(i, 1, n)
{
scanf("%lld", &a[i]);
a[i]++;//所有 a[i] + 1,避免 0
}
rep(i, 1, n)
{
cnt[a[i]] += query(n + 1) - query(a[i]); //树状数组类似于桶,每次向里面插入元素,query查询逆序对
add(a[i], 1);
}
int ans = 0;
rep(i, 1, n)
{
printf("%lld\n", ans);
ans += cnt[i]; //每次累计 cnt[i] 要在输出后再累计!
}
return 0;
}