题意:给定一个序列,我们根据这个序列来建立一张n个节点的图如下:
1.对于1 <= i <= n,我们找到一个最大的j,满足1 <= j < i并且pj > pi,在节点i和节点j之间连一条边
2.对于1 <= i <= n,我们找到一个最小的j,满足i < j <= n并且pj > pi,在节点i和节点j之间连一条边
求所有序列中,满足含有简单环的情况,数据很大,需要模上1e9+7
分析:我们先来看看样例给出的4,答案为16,全集为4 * 3 * 2 * 1,所有序列个数为24,说明不合法的情况相对于全集来说很少,说明我们可以尝试用全集-不合法的情况来算出合法的情况。我们来看看[3, 1, 2, 4],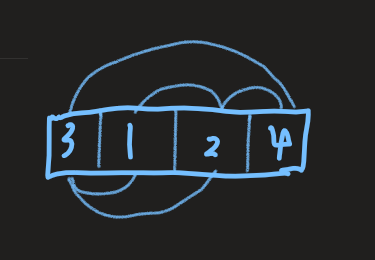 ,存在简单环的情况,
,存在简单环的情况,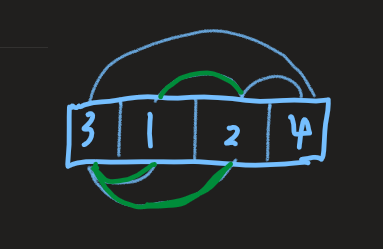 ,从1开始到2,从2再到3,再回到1。对于题目来说,一个点会连向最靠近它的大于它的值的点,不失一般性,我们假设如下:
,从1开始到2,从2再到3,再回到1。对于题目来说,一个点会连向最靠近它的大于它的值的点,不失一般性,我们假设如下: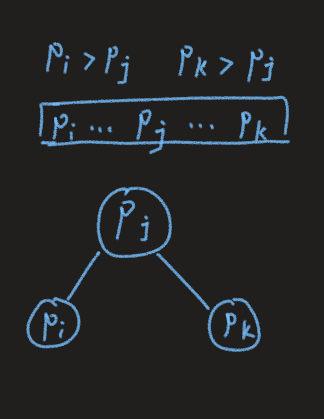 ,然后假设pi < pk,那么pi和pk之间也会连一条边,这样就存在一个简单环了。pi和pk是最靠近pj的并且大于pj的数,我们可以发现,(pi, pj),(pj, pk)之间的点都是小于左右两个端点的值的。我们可以得到不合法的情况即是一个单峰序列,单峰序列的方案数为(2^{n-1})。那么合法的方案数即为(n! - 2^{n-1})。
,然后假设pi < pk,那么pi和pk之间也会连一条边,这样就存在一个简单环了。pi和pk是最靠近pj的并且大于pj的数,我们可以发现,(pi, pj),(pj, pk)之间的点都是小于左右两个端点的值的。我们可以得到不合法的情况即是一个单峰序列,单峰序列的方案数为(2^{n-1})。那么合法的方案数即为(n! - 2^{n-1})。
单峰排列的个数:假设f[i]为1~i构成的单峰排列方案数,那么我们f[i + 1]为把i + 1插入到f[i]的排列的峰顶i的左右两侧,方案数则为f[i] * 2,即f[i + 1] = f[i] * 2。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
const int mod = 1e9 + 7;
int qmi(int a, int b)
{
int res = 1;
while (b)
{
if (b & 1) res = (ll)res * a % mod;
a = (ll)a * a % mod;
b >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
int res = 1;
for (int i = n; i >= 1; --i)
{
res = ((ll)res * i) % mod;
}
res = (((ll)res - qmi(2, n - 1)) % mod + mod) % mod;
cout << res << endl;
return 0;
}