隐马尔科夫模型（HMM）与词性标注问题

一、马尔科夫过程：

　　在已知目前状态（现在）的条件下，它未来的演变（将来）不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中，有很多过程都是马尔可夫过程，如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等，都可视为马尔可夫过程。

二、马尔科夫链：

　　时间和状态都是离散的马尔可夫过程称为马尔可夫链,简记为Xn=X(n),n=0,1,2…

三、马尔可夫模型（Markov Model）：

　　是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。

　　一个马尔科夫过程包括一个初始向量和一个状态转移矩阵。关于这个假设需要注意的一点是状态转移概率不随时间变化。

四、隐马尔科夫模型：

（1）概述

　　在某些情况下马尔科夫过程不足以描述我们希望发现的模式。譬如，一个隐居的人可能不能直观的观察到天气的情况，但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合，一个可以观察到的状态集合（海藻的状态）和一个隐藏的状态（天气的状况）。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。

其中，隐藏状态的数目和可以观察到的状态的数目可能是不一样的。在语音识别中，一个简单的发言也许只需要80个语素来描述，但是一个内部的发音机制可以产生不到80或者超过80种不同的声音。同理，在一个有三种状态的天气系统（sunny、cloudy、rainy）中，也许可以观察到四种潮湿程度的海藻（dry、dryish、damp、soggy）。在此情况下，可以观察到的状态序列和隐藏的状态序列是概率相关的。于是我们可以将这种类型的过程建模为一个隐藏的马尔科夫过程和一个和这个马尔科夫过程概率相关的并且可以观察到的状态集合。

（2）HMM的模型表示

　　HMM由隐含状态S、可观测状态O、初始状态概率矩阵pi、隐含状态概率转移矩阵A、可观测值转移矩阵B（混淆矩阵）组成。

　　pi和A决定了状态序列，B决定了观测序列，因此，HMM可以由三元符号表示：

　　

　　HMM的两个性质：

　　1. 齐次假设：

　　

　　2.观测独立性假设：

　　

　　齐次假设：本质就是时刻t的状态为qi，原本是要给定t时刻之前的所有状态和观测才可以确定，但是其实我们给出前一个时刻t-1的状态就可将t时刻与之前隔断，也就是说我们假设t时刻与t-1之前的所有状态和观测是独立的。

　　观测独立性假设：本质就是t时刻的观测为ot，原本是要给定包括t时刻和t时刻之前所有的观测和状态才能确定，现在我们给定t时刻状态qi就将ot与前边隔断，也就是说我们假设t时刻的观测ot与t时刻之前的所有状态和观测是独立的

 （3）HMM的三个问题

　　概率计算问题：前向-后向算法----动态规划

　　给定模型 λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，计算模型λ下观测O出现的概率P(O | λ)

　　学习问题：Baum-Welch算法----EM算法

　　已知观测序列O={o1, o2, o3 ...}，估计模型λ = (A, B, π)的参数，使得在该参数下该模型的观测序列P(O | λ)最大

　　预测问题：Viterbi算法----动态规划

　　解码问题：已知模型λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，求给定观测序列条件概率P(I | O，λ)最大的状态序列I

a)概率计算问题

　　对于概率计算问题，可以采用暴力计算法、前向算法和后向算法

　　暴力法：

　　问题：已知HMM的参数 λ，和观测序列O = {o₁, o₂, ...,o_T}，求P(O|λ)

　　思路：--------------------------------------------------------------------------

1. 列举所有可能的长度为T的状态序列I = {i₁, i₂, ..., i_T}；每个i都有N个可能的取值。
2. 求各个状态序列I与观测序列 的联合概率P(O,I|λ)；
3. 所有可能的状态序列求和∑_I P(O,I|λ)得到P(O|λ)。

步骤：

1，最终目标是求O和I同时出现的联合概率，即：

P(O,I|λ)= P(O|I, λ)P(I|λ)

那就需要求出P(O|I, λ) 和 P(I|λ)。

2，求P(I|λ) ，即状态序列I = {i₁,i₂, ..., i_T} 的概率：

2.1，P(I|λ) = P(i₁,i₂, ..., i_T |λ)

=P(i₁ |λ)P(i₂, i₃, ..., i_T |λ)

=P(i₁ |λ)P(i₂ | i_1, λ)P(i₃, i₄, ..., i_T |λ)

=......

=P(i₁ |λ)P(i₂ | i_1, λ)P(i₃ | i_2, λ)...P(i_T | i_T-1, λ)

而上面的P(i₁ |λ) 是初始为状态i₁的概率，P(i₂ | i_1, λ) 是从状态i1转移到i2的概率，其他同理，于是分别使用初始概率分布π 和状态转移矩阵A，就得到结果：

PS：上面的a_i1i2代表A的第i₁行第i₂列。

3，P(O|I, λ)，即对固定的状态序列I，观测序列O的概率是：

4，代入第一步求出P(O,I|λ)。

5，对所有可能的状态序列I求和得到观测序列O的概率P(O|λ)：

时间复杂度：

每个时刻有n个状态，一共有t个时刻，而根据上面的第5步可以知道每个时刻状态a_i相乘的复杂度为n^T，然后乘以各个对应的b，所以时间复杂度大概为：O(Tn^T)阶

概率消失：

可以通过取对数，防止P的值过小。

　　前向概率：

 　　前向概率的定义：当第t个时刻的状态为i时，前面的时刻分别观测到q1,q2, ..., qt的概率。

　　

 　　初值：

　　

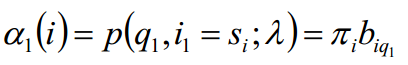
　　递推：

　　

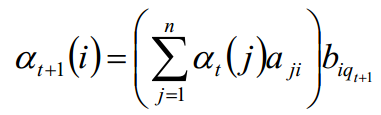
　　最终值：

　　

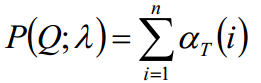
　　时间复杂度：

　　由公式可见，括号里面的时间复杂度为N^2，迭代过程中，又乘上T个时刻的b，因此，时间复杂度为O(TN^2)阶的。

       对于暴力法和前向算法时间复杂度的理解：

　　对于两种算法，其实本质上都是通过状态 x 观测概率获得的概率值，只不过区别在于，前向算法将每一个时刻的状态概率先进行相加然后乘以观测概率，获得最终值。

　　可以理解为：a1*a2*a3...    如果ai有n种取值，其复杂度为 O(n^T)

　　　　　　　　对于另一种表达方式： α*a1  同理 α有n种取值，ai有n种取值，那么复杂度为 O(n^2)

时间复杂度计算：

后向概率和前向概率类似，此处不赘述。

b)学习问题

　　学习问题分两种：

•  观测序列和隐状态序列都给出，求HMM。这种学习是监督学习。
•  给出观测序列，但没给出隐状态序列，求HMM。这种学习是非监督学习，利用Baum-Welch(鲍姆-韦尔奇)算法。

 　　对于监督学习，利用大数定律“频率的极限是概率”即可求解：

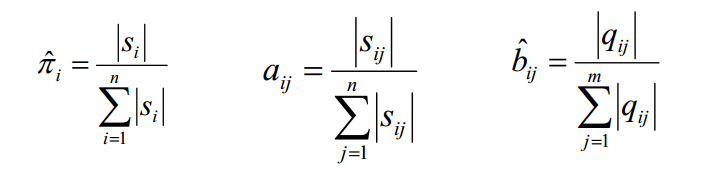
　　 对于非监督学习，一般采用Baum-Welch算法。

 　　对于观测数据Q、隐藏状态I、概率P(Q, I ;λ)即为暴力法的表达式，其对数似然函数为：ln(P(Q, I ;λ))，然后用EM算法求解即可。

　　求 π：利用约束条件：所有π_i的和为1。

　　

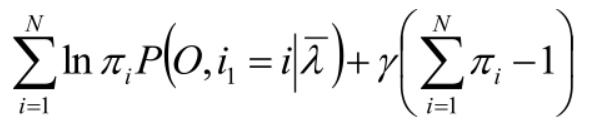
　　拉格朗日函数求解：

　　

　　

　　同理：

　　

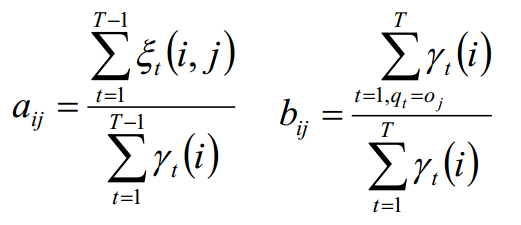
c)预测问题：

　　对于预测问题，本文主要讲Viterbi算法。Viterbi算法实际是用动态规划的思路求解HMM预测问题。求出概率最大的路径，每个路径对应一个状态序列。

 　　盒子和球模型λ= (A, B,π)，状态集合Q={1, 2, 3}，观测集合V={白，黑}，已知观测序列“白黑白白黑”，求最优的隐藏状态

  

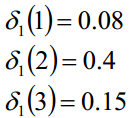
 　　同理：

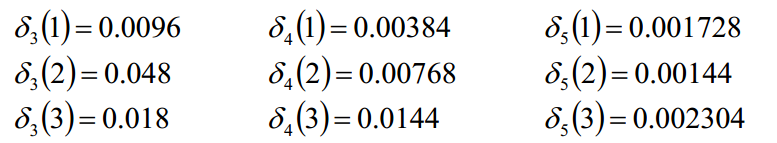
　　可以看到结果如图：

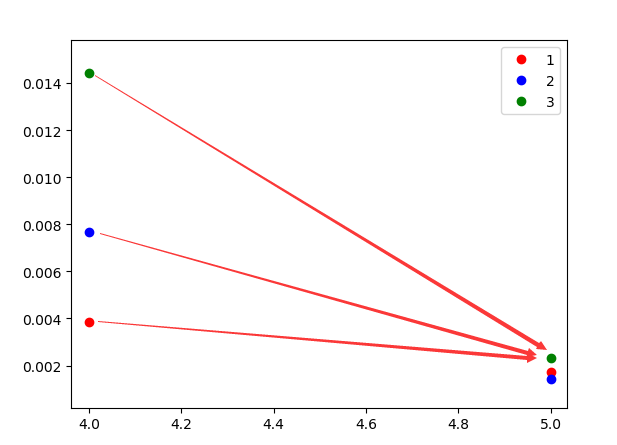
　　我们从后往前查询，第5时刻最大概率的状态为3，然后往前推导，究竟第5个状态是从哪一个状态的来的呢？

　　max{  0.00384*0.1   0.00768*0.6   0.0144*0.3 } 可以看到，应该取状态2 -> 3才是最大的，故第4个时刻的状态为2。

　　最终求得最优状态为：2 3 2 2 3

五、viterbi用于词性标注

　　词性标注问题映射到隐马模型可以表述为：模型中状态(词性)的数目为词性符号的个数N；从每个状态可能输出的不同符号(单词)的数目为词汇的个数M。假设在统计意义上每个词性的概率分布只与上一个词的词性有关(即词性的二元语法)，而每个单词的概率分布只与其词性相关。那么，我们就可以通过对已分词并做了词性标注的训练语料进行统计，统计出HMM的参数 λ，当然这就是上述学习问题。

　　然后可以根据已知的词语，通过viterbi算法，求出每个词语对应的词性，即完成词性标注。