1、图像锐化理论
图像锐化的目的是使图像变得清晰起来,锐化主要用于增强图像的灰度跳变部分,这一点与图像平滑对灰度跳变的抑制正好相反。锐化提高图像的高频分量,增加灰度反差增强图像的边缘和轮廓,以便后期图像识别。
在图像增强过程中,常用平滑算法来消除噪声,平滑属于低通滤波,图像的能量主要集中在低频部分,噪声所在频段主要在高频部分,同时图像的边缘也集中在高频部分,这意味着图像平滑后,高频被衰减轮廓会出现模糊。图像锐化就是为了减少这种现象,通过高通滤波使图像边缘和轮廓变得清晰。
2、一阶微分图像增强--梯度算子

其中:
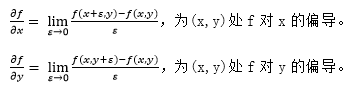
梯度的方向就是函数f(x,y)最大变化率的方向。梯度的幅值作为最大变化率大小的度量,值为:

离散的二维函数f(i,j),可以用有限差分作为梯度的一个近似值。
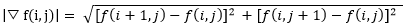
为了简化计算,可以用绝对值来近似。
|▽f(i,j)|= |f(i+1,j)-f(i,j)| +|f(i,j+1)-f(i,j)|
2.1 Robert算子
|▽f(i,j)|= |f(i+1,j+1)-f(i,j)| +|f(i,j+1)-f(i+1,j)|
上面算式采用对角相差的差分法来代替微分,写为滤波模板形式为:
 其中w1对接近45°的边缘有较强响应,w2对接近-45°的边缘有较强响应。
其中w1对接近45°的边缘有较强响应,w2对接近-45°的边缘有较强响应。
imgPath = 'E:opencv_picsrc_picpic6.bmp';
img = imread(imgPath);
img=rgb2gray(img);
w1 =[-1,0; 0,1];
w2 =[0,-1; 1, 0];
G1=imfilter(img, w1, 'corr', 'replicate');
G2=imfilter(img, w2, 'corr', 'replicate');
G=abs(G1)+abs(G2);
subplot(2,2,1),imshow(img), title('原始图像');
subplot(2,2,2),imshow(abs(G1)), title('w1图像');
subplot(2,2,3),imshow(abs(G2)),title('w2滤波');
subplot(2,2,4),imshow(G),title('Robert交叉梯度图像');

可见w1滤波后45°的边缘被突出,w2滤波后-45°的边缘被突出。Robert交叉滤波后全部边缘突出显示。
2.2 Sobel算子
滤波时一般更多使用奇数尺寸的模板,下面是Sobel算子。
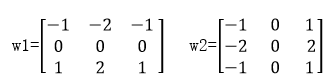
imgPath = 'E:opencv_picsrc_picpic6.bmp';
img = imread(imgPath);
img=rgb2gray(img);
w1 =[-1,-2,-1; 0,0,0; 1,2, 1];
w2 =[ -1,0,1; -2,0,2; -1,0,1];
G1=imfilter(img, w1);
G2=imfilter(img, w2);
G=abs(G1)+abs(G2);
subplot(2,2,1),imshow(img), title('原始图像');
subplot(2,2,2),imshow(abs(G1)), title('w1图像');
subplot(2,2,3),imshow(abs(G2)),title('w2滤波');
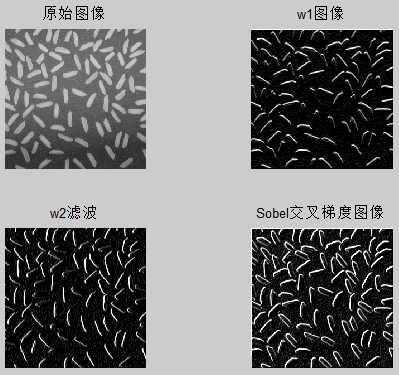
subplot(2,2,4),imshow(G),title('Sobel交叉梯度图像');
同Robert算子,w1滤波后45°的边缘被突出,w2滤波后-45°的边缘被突出。Sobel交叉滤波后全部边缘突出显示。
3、二阶微分滤波--拉普拉斯算子
二维函数f(x,y)在二阶微分(拉普拉斯算子)的定义为:
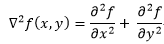

将上式相加后就得到拉普拉斯算子:
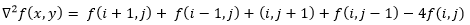
对应的滤波模板如下:
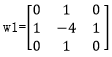
考虑到求绝对值计算梯度,正负系数图形的响应一样,上面的模板也可以表示为:

上面的模板具有对称性,所以求一次滤波就可以,不需要像一阶微分那样计算2次。
imgPath = 'E:opencv_picsrc_picpic6.bmp';
img = imread(imgPath);
img=rgb2gray(img);
w1 =[0,1,0; 1,-4,1; 0,1,0];
w2 =[0,-1,0; -1,4,-1; 0,-1,0];
w3 =[1,4,1; 4,-20,4; 1,4,1];
G1=imfilter(img, w1, 'corr', 'replicate');
G2=imfilter(img, w2, 'corr', 'replicate');
G3=imfilter(img, w3, 'corr', 'replicate');
subplot(2,2,1),imshow(img,[]), title('原始图像');
subplot(2,2,2),imshow(abs(G1)), title('w1图像');
subplot(2,2,3),imshow(abs(G2)),title('w2滤波');
subplot(2,2,4),imshow(abs(G3)),title('加权二阶滤波');
二阶滤波比之前的一阶滤波锐化程度更加强烈,留下了非常清晰的边缘图案。w1和w2滤波的方向性不明显图像基本一致,仅w2滤波图像的轮廓更加深一些。

使用imsharpen对图像进行锐化,对锐化强度参数进行控制,可见太高的锐化强度导致图像出现“纹理”,效果变差。
b1=imsharpen(img,'Radius',1,'Amount',0.2);
b2=imsharpen(img,'Radius',1,'Amount',2);
b3=imsharpen(img,'Radius',1,'Amount',1);
subplot(1,4,1),imshow(img), title('原始图像');
subplot(1,4,2),imshow(b1), title('imsharpen图像1');
subplot(1,4,3),imshow(b2), title('imsharpen图像2');
subplot(1,4,4),imshow(b3), title('imsharpen图像3');

4、锐化图像后续处理
无论一阶微分算子还是二阶微分算子,各系数之和都为0,说明算子在灰度恒定区域的响应为0,即锐化后的图像,在原图比较平坦的区域几乎都变为黑色,而在图像边缘,灰度跳变点的细节被突出显示。一般图像锐化是希望增强图像的边缘和细节,而非将平滑区域的灰度信息丢失。因此,可以用原图像加上锐化后的图像,得到比较理想的结果。
使用Sobel算子锐化和matlab内置锐化函数锐化之后的图像对比,下图是内置函数锐化结果:
b=imsharpen(img,'Radius',2,'Amount',1);
subplot(1,2,1),imshow(img), title('原始图像');
subplot(1,2,2),imshow(b), title('imsharpen图像');

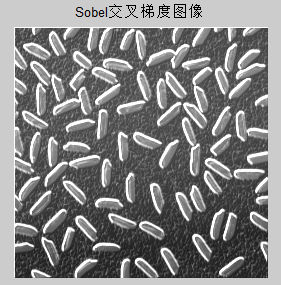
imsharpen滤波图像明显比算子锐化的图像亮度更高,保留了原图比较平坦的部分,比如背景图部分。如果希望上面的滤波函数也达到这个效果,只需要把原图加上滤波后的图像即可,系数是为了防止溢出,比如下面的例子。使用函数为imshow(G+0.7*img),title('Sobel交叉梯度图像')。
5、参考文献
1、MATLAB--数字图像处理 图像锐化(原理篇)
https://www.csdn.net/gather_24/MtjaMg4sMjg1OS1ibG9n.html
2、imsharpen
https://ww2.mathworks.cn/help/images/ref/imsharpen.html
3、《数字图像处理与机器视觉》
第二版。 张铮、徐超、任淑霞、韩海玲等编著。
尊重原创技术文章,转载请注明。