初始化有三点个要求,
一个是不能有对称性,比如全为0.这样的反向传播对每一个单元学习到的结果都一样。没有区分度学习不到东西。
另一个要求是避免落入激活函数饱和区,导致梯度学习太慢。
第三点对于深度网络中的每一层,它们的输出方差应该尽量相同,满足学习到的目标分布和原始分布一致(那我们将其都转换到均值0方差1)。
满足第一点,用随机化,使用高斯分布,均匀分布都行。
满足第二点,让它的均值0方差1即可,不会跳跃到饱和区(sigmoid最明显,因此后来用ReLU了)。
满足第三点,采用Xavier初始化方法,输出输入方差一致。
详细说一下
Xavier
我们假设输入输出的单元,均值0方差1。
对于一个线性激活函数来说,n个输入单元一个偏置b
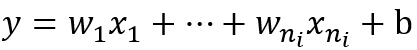
它的方差计算
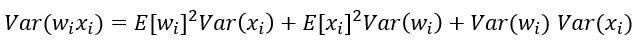
因为我们假设均值为0,有
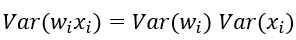
同时w的产生和输入的x自然是没什么关系,独立分布。
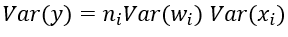
前向传播,反向传播的方差计算类似,因此满足下面即可。
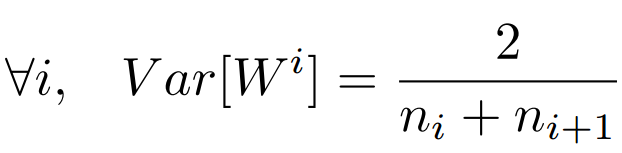
具体来说,对于sigmoid , (W^{[l]}=np.random.randn(shape)*np.sqrt(frac{1}{n^{[l-1]}}))
ReLU, (W^{[l]}=np.random.randn(shape)*np.sqrt(frac{2}{n^{[l-1]}}))