第一章 函数

一 函数概念

  

二  函数的特性

 

 

奇函数关于原点对称

偶函数关于轴对称

三 函数的类型

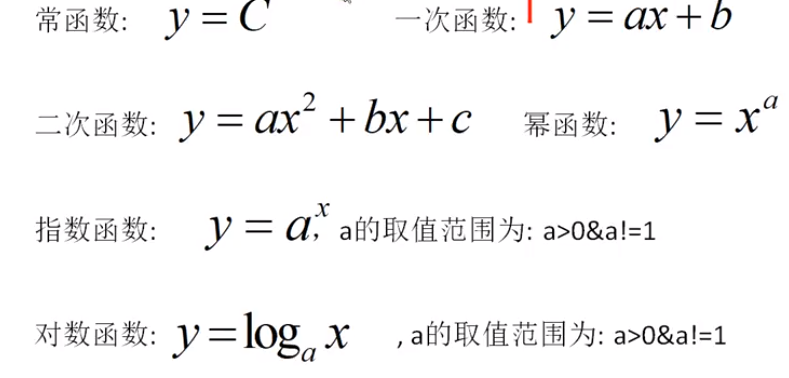
四 指数函数

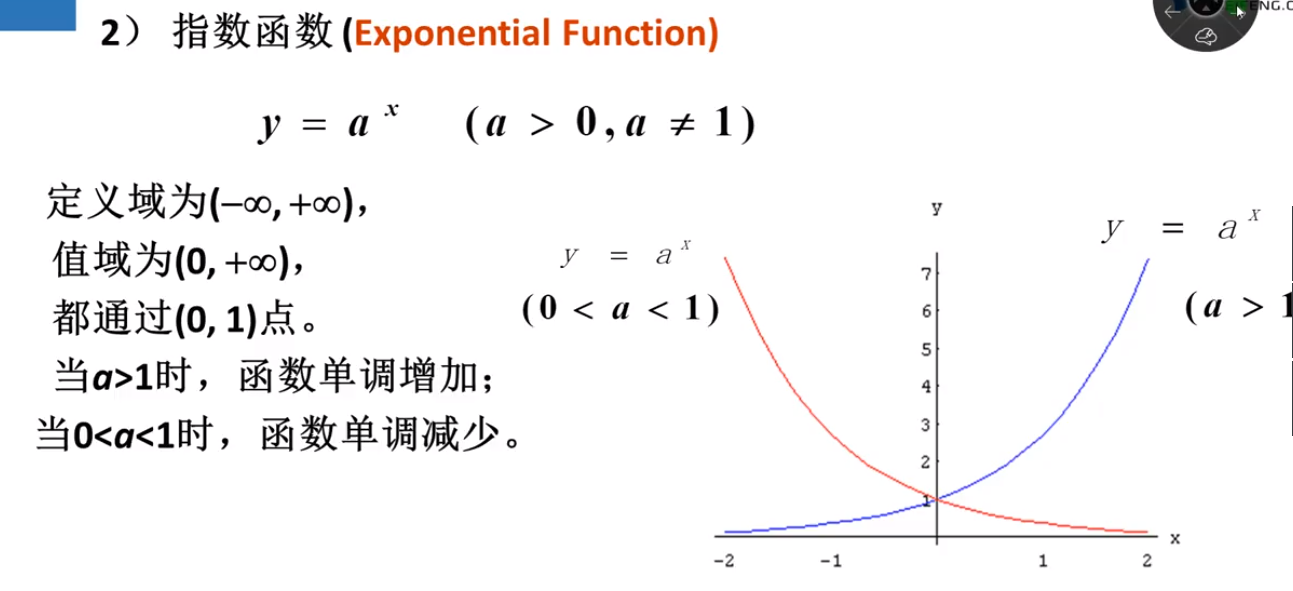
指数函数运算法则 ：

①

②

③

④

与

的图像关于y轴对称

 

五 对数函数

 

 

 

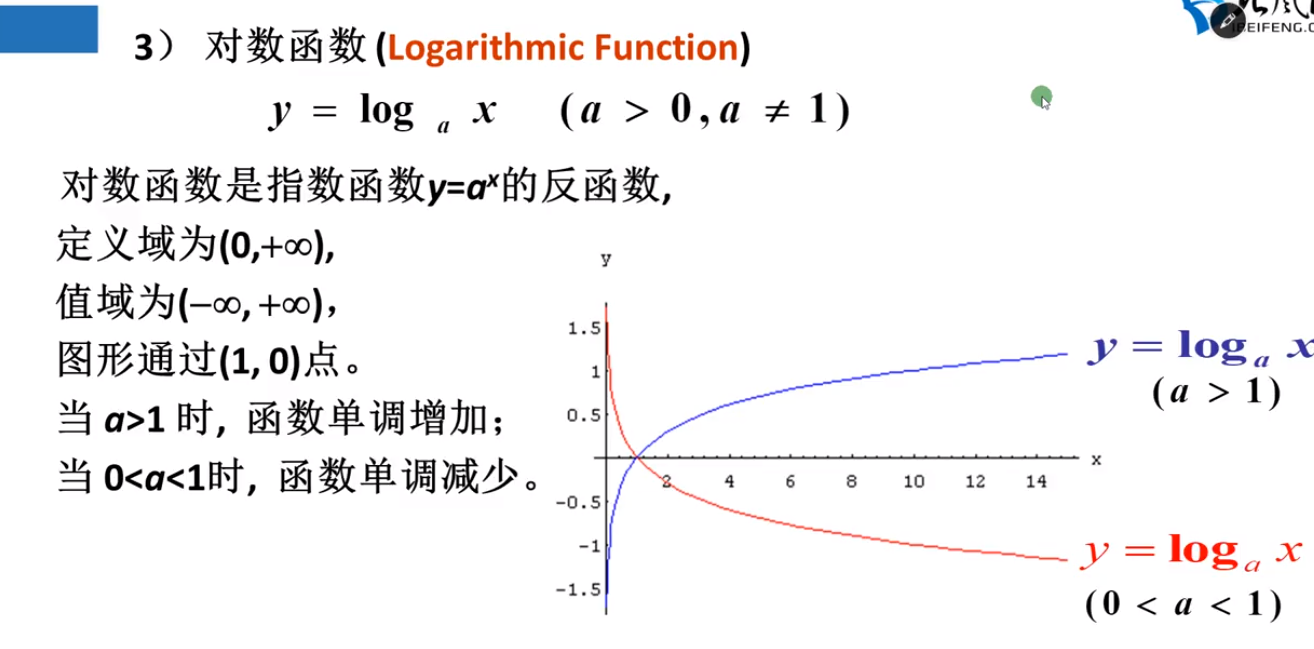
注意：负数和0没有对数。

两句经典话：底真同对数正，底真异对数负。解释如下：

也就是说：若y=log_ab （其中a>0，a≠1，b>0）

当0<a<1， 0<b<1时，y=log_ab>0;

当a>1， b>1时，y=log_ab>0;

当0<a<1， b>1时，y=log_ab<0;

当a>1， 0<b<1时，y=log_ab<0。

 

 

 

对数公式

• 
• 
• 

六 反函数

 

 

 

 

 

 

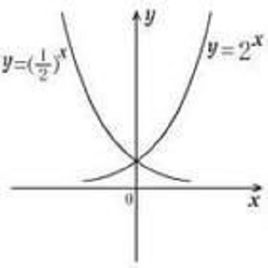
指数函数和对数函数互为反函数

 

 

反函数：

一般来说，设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作y=f^(-1)(x) 。反函数y=f ^(-1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域。最具有代表性的反函数就是对数函数与指数函数。

 

反函数的性质有：

①函数f(x)与它的反函数f-1(x)图象关于直线y=x对称；函数及其反函数的图形关于直线y=x对称

②函数存在反函数的充要条件是，函数的定义域与值域是一一映射；

③一个函数与它的反函数在相应区间上单调性一致；

④一个函数在其单调区间一定存在反函数。

⑤y=f(x)的图像与它的反函数的图像是关于y=x对称的。

⑥如果一个函数的反函数是它本身，则它的图像自身是关于y=x对称的。

 

 7， 三角函数

 

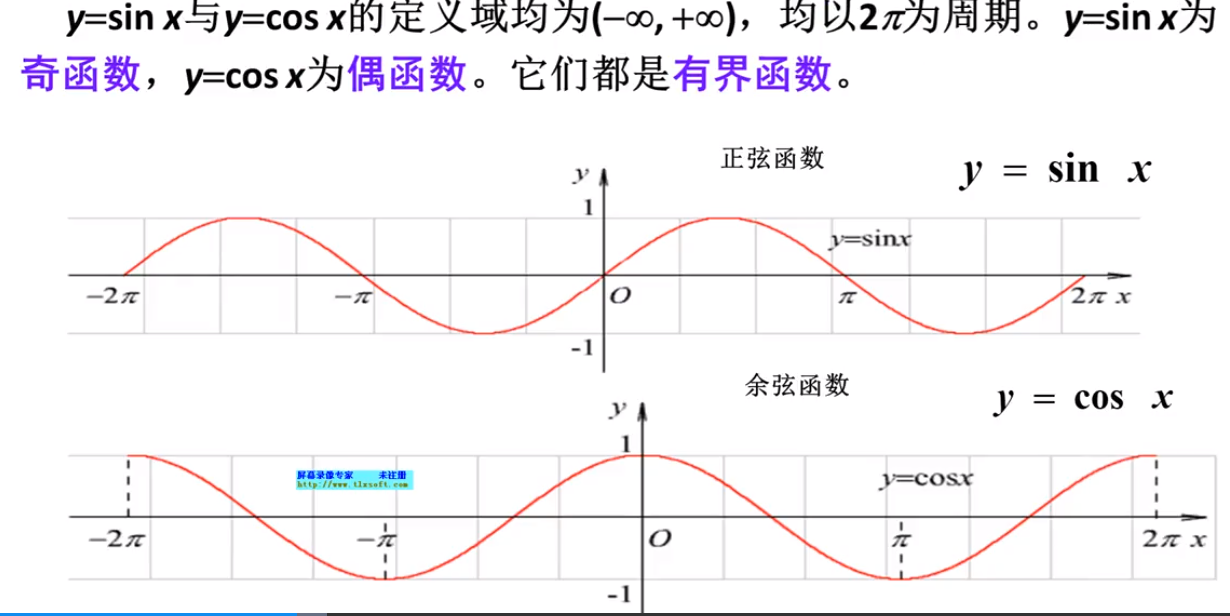
    正弦函数

    余弦函数

 

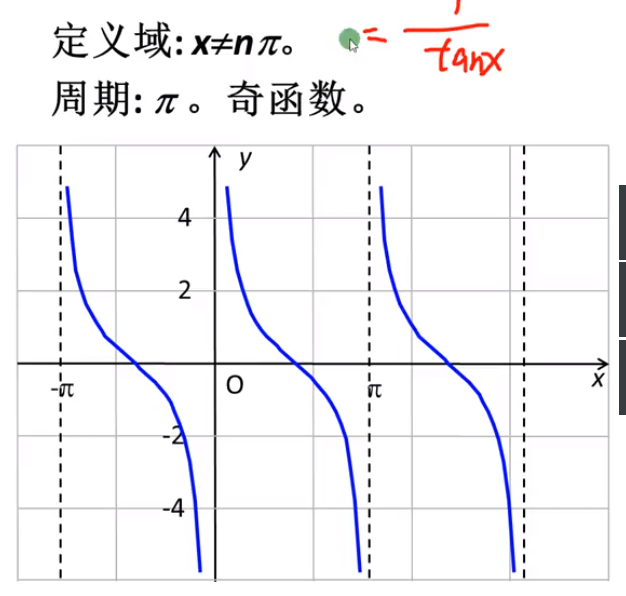
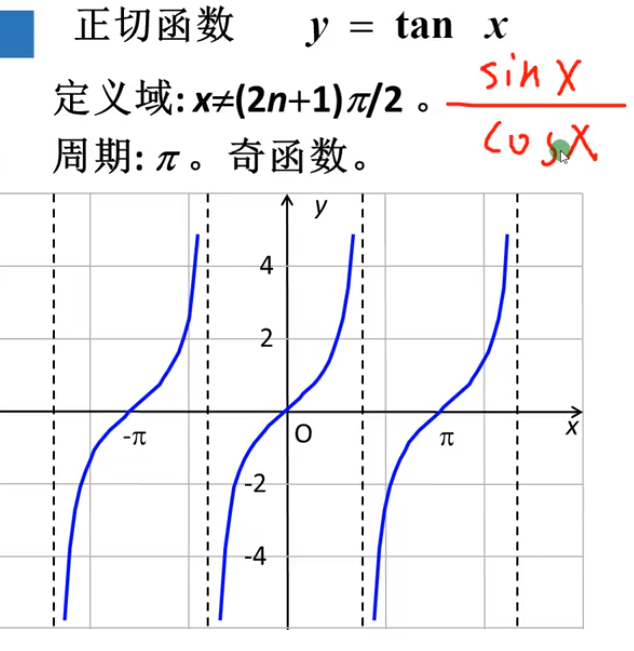
正切函数

 

 

 

 

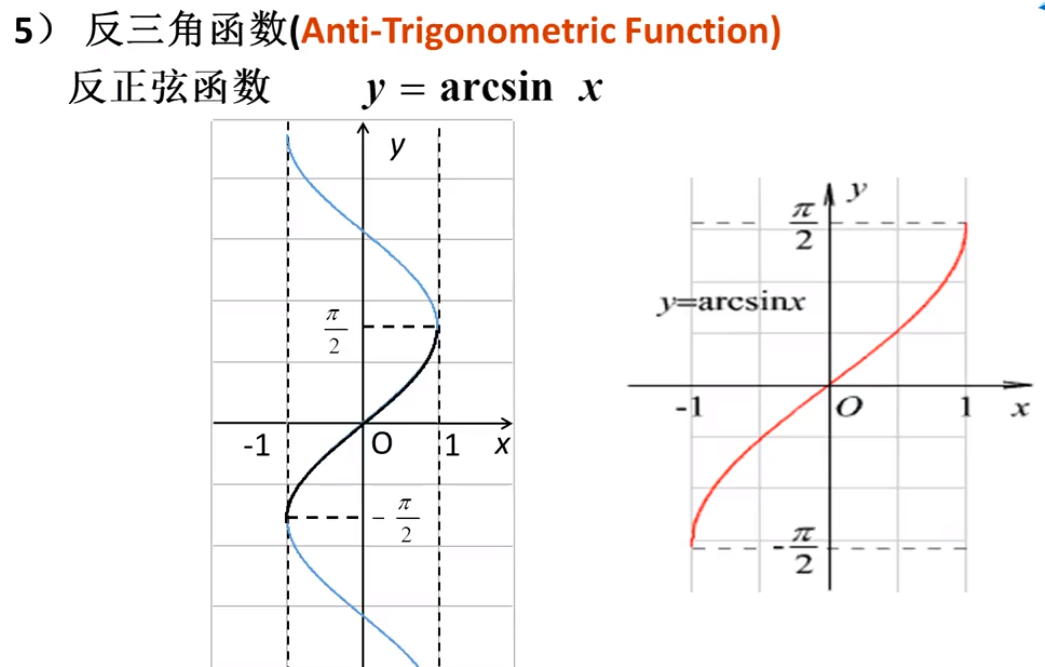
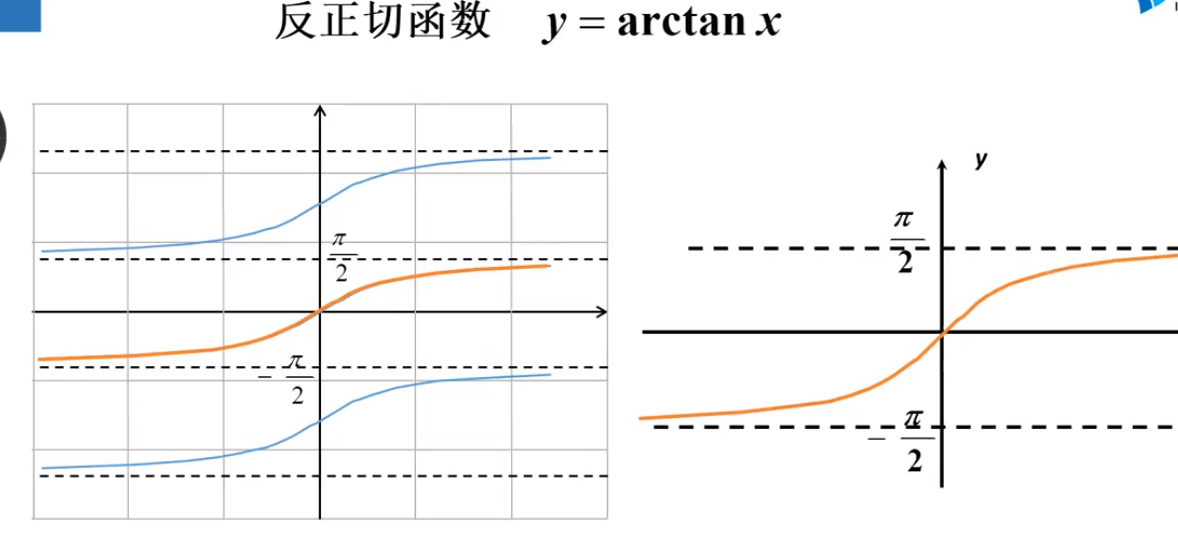
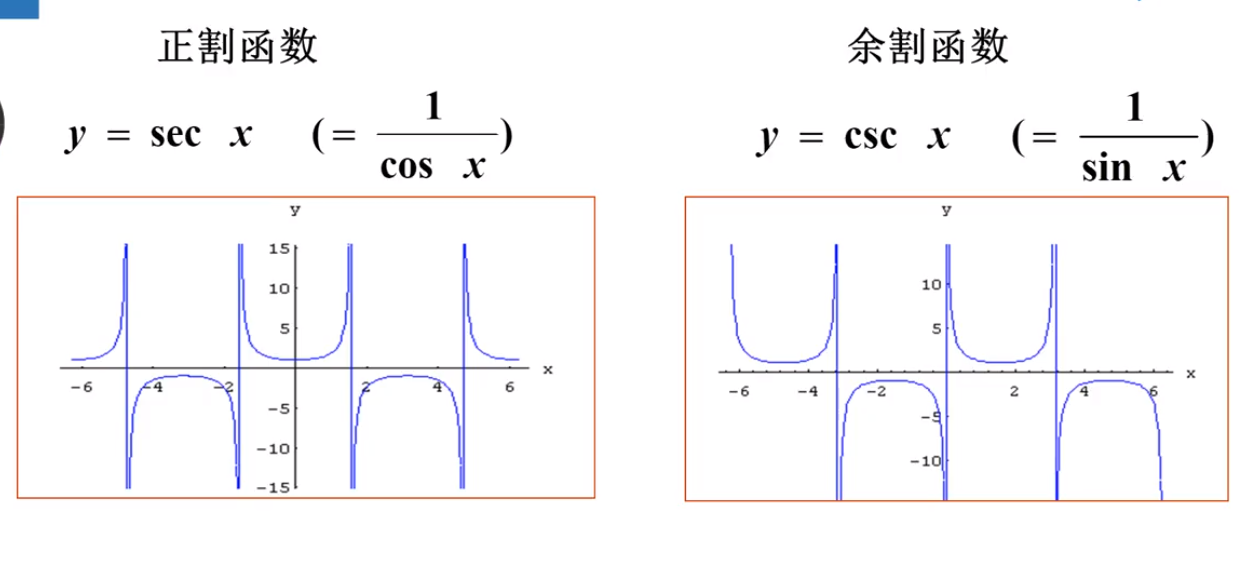
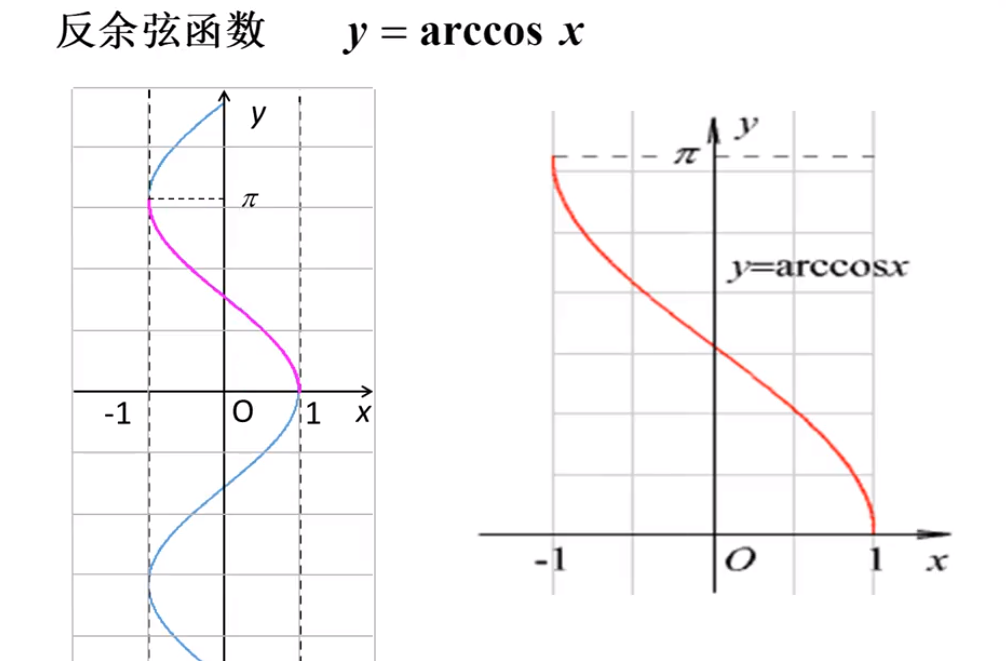
八 复合函数