总结: NLLLoss, CrossEntropyLoss, BCELoss, BCEWithLogitsLoss比较，以及交叉熵损失函数推导

一、pytorch中各损失函数的比较

Pytorch中Softmax、Log_Softmax、NLLLoss以及CrossEntropyLoss的关系与区别详解

Pytorch详解BCELoss和BCEWithLogitsLoss

总结这两篇博客的内容就是：

1. CrossEntropyLoss函数包含Softmax层、log和NLLLoss层，适用于单标签任务，主要用在单标签多分类任务上，当然也可以用在单标签二分类上。
2. BCEWithLogitsLoss函数包括了Sigmoid层和BCELoss层，适用于二分类任务，可以是单标签二分类，也可以是多标签二分类任务。

• 以上这几个损失函数本质上都是交叉熵损失函数，只不过是适用范围不同而已。

第一条的原因是：

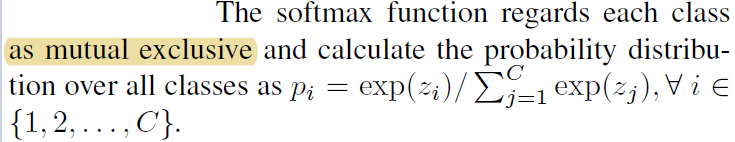
也就是说，各个class的得分是互斥的，这个class得分多了，另个class的得分会减少。

第二条的原因是：

也就是说，各个class的得分是独立的，互不影响，所以可以进行多标签预测。

二、程序示例

在使用中，最常遇到的情况是，CrossEntropyLoss的input是一个二维张量，target是一维张量，例如：

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)   # 3个样本，5个类别
target = torch.empty(3, dtype=torch.long).random_(5)   
# torch.long表示长整型，torch.empty(3)表示产生一维向量，长度为3，元素内容为空。
# random_(5)表示用0到4的整数去填充3个空元素。之所以是整数，是因为前面规定了torch.long。

output = loss(input, target)
output.backward()

CrossEntropyLoss的计算公式为(本质上是交叉熵公式+softmax公式)：

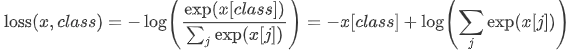
BCEWithLogitsLoss和BCELoss的input和target必须保持维度相同，即同时是一维张量，或者同时是二维张量，例如：

m = nn.Sigmoid()
loss = nn.BCELoss()

# input和target同为一维张量
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)   # 单标签二分类任务
output = loss(m(input), target)
output.backward()

# input和target同为二维张量
input = torch.randn([5, 3], requires_grad=True)
target = torch.empty([5, 3]).random_(2)   # 多标签二分类任务
output = loss(m(input), target)
output.backward()

-------------------------------------------

loss = nn.BCEWithLogitsLoss()

# input和target同为一维张量
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)   # 单标签二分类任务
output = loss(input, target)
output.backward()

# input和target同为二维张量
input = torch.randn([5,3], requires_grad=True)
target = torch.empty([5,3]).random_(2)   # 多标签二分类任务
output = loss(input, target)
output.backward()

三、交叉熵损失函数的推导

以下的内容摘自知乎：交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）

对于二分类问题，假设是猫和狗的分类问题，则p(x=猫)=1-p(x=狗)，同样地q(x=猫)=1-q(x=狗)，所以，对于某一张图片(样本)，它的损失可通过如下公式计算：

这个二分类公式其实是cross entropy between two Bernoulli distribution。这个公式不仅可以用于单标签的二分类问题，也可以用于多标签的二分类问题。在pytorch的BCEWithLogitsLoss函数或者BCELoss函数中，实际计算公式是这样的：

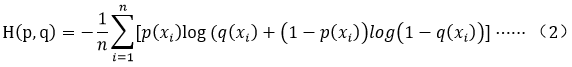
式中，n是指总的类别数目，这个公式指的是单个样本的损失。对单标签二分类时，即当n=2时，(2)式和(1)式等价，证明：

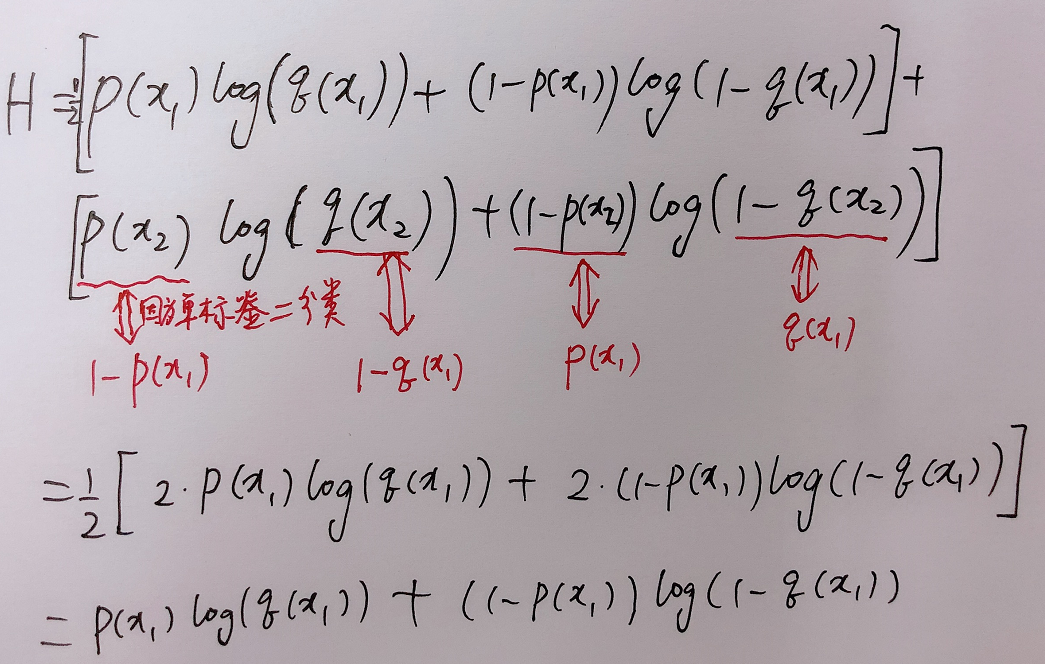
简单的算例证明可以参考知乎：pytorch中的损失函数总结 第6小节