感知器做二分类的原理及python numpy实现

本文目录：

1. 感知器

2. 感知器的训练法则

3. 梯度下降和delta法则

4. python实现

1. 感知器^[1]

人工神经网络以感知器（perceptron）为基础。感知器以一个实数值向量作为输入，计算这些输入的线性组合，然后如果结果大于某个阈值，就输出1，否则输出-1（或0）。更精确地，如果输入为$x_1$到$x_n$，那么感知器计算的输出为：

 其中，$w_i$是实数常量，叫做权值，用来决定输入$x_i$对感知器输出的贡献率。因为仅以一个阈值来决定输出，我们有时也把这种感知器叫做硬限幅感知器，当输出为1和-1时，也叫做sgn感知器（符号感知器）。

 2. 感知器的训练法则^[1]

感知器的学习任务是决定一个权向量，它可以是感知器对于给定的训练样例输出正确的1或-1。为得到可接受的权向量，一种办法是从随机的权值开始，然后反复应用这个感知器到每一个训练样例，只要它误分类样例就修改感知器的权值。重复这个过程，直到感知器正确分类所有的训练样例。每一步根据感知器训练法则(perceptron Iraining rule) 来修改权值：${w_{i + 1}} leftarrow {w_i} + Delta {w_i}$，其中$Delta {w_i} = eta (t - o){x_i}$，$eta$是学习速率，用来缓和或者加速每一步调整权值的程度。

 3. 梯度下降和delta法则^[1]

 

 

 

 

 

 

 4. python实现^[2]

训练数据：总共500个训练样本，链接https://pan.baidu.com/s/1qWugzIzdN9qZUnEw4kWcww，提取码：ncuj

损失函数：均方误差（MSE）

 代码如下：

import numpy as np
import matplotlib.pyplot as plt


class hardlim():
    def __init__(self, path):
        self.path = path

    def file2matrix(self, delimiter):
        fp = open(self.path, 'r')
        content = fp.read()              # content现在是一行字符串，该字符串包含文件所有内容
        fp.close()
        rowlist = content.splitlines()   # 按行转换为一维表
        # 逐行遍历
        # 结果按分隔符分割为行向量
        recordlist = [list(map(float, row.split(delimiter))) for row in rowlist if row.strip()]
        return np.mat(recordlist)

    def drawScatterbyLabel(self, dataSet):
        m, n = dataSet.shape
        target = np.array(dataSet[:, -1])
        target = target.squeeze()        # 把二维数据变为一维数据
        for i in range(m):
            if target[i] == 0:
                plt.scatter(dataSet[i, 0], dataSet[i, 1], c='blue', marker='o')
            if target[i] == 1:
                plt.scatter(dataSet[i, 0], dataSet[i, 1], c='red', marker='o')

    def buildMat(self, dataSet):
        m, n = dataSet.shape
        dataMat = np.zeros((m, n))
        dataMat[:, 0] = 1
        dataMat[:, 1:] = dataSet[:, :-1]
        return dataMat

    def classfier(self, x):
        x[x >= 0.5] = 1
        x[x < 0.5] = 0
        return x


if __name__ == '__main__':
    hardlimit = hardlim('testSet.txt')

    print('1. 导入数据')
    inputData = hardlimit.file2matrix('	')
    target = inputData[:, -1]
    m, n = inputData.shape
    print('size of input data: {} * {}'.format(m, n))

    print('2. 按分类绘制散点图')
    hardlimit.drawScatterbyLabel(inputData)

    print('3. 构建系数矩阵')
    dataMat = hardlimit.buildMat(inputData)

    alpha = 0.1                 # learning rate
    steps = 600                 # total iterations
    weights = np.ones((n, 1))   # initialize weights
    weightlist = []

    print('4. 训练模型')
    for k in range(steps):
        output = hardlimit.classfier(dataMat * np.mat(weights))
        errors = target - output
        print('iteration: {}  error_norm: {}'.format(k, np.linalg.norm(errors)))
        weights = weights + alpha*dataMat.T*errors  # 梯度下降
        weightlist.append(weights)

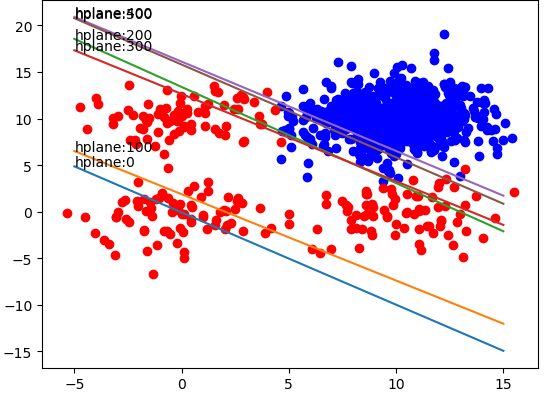
    print('5. 画出训练过程')
    X = np.linspace(-5, 15, 301)
    weights = np.array(weights)
    length = len(weightlist)
    for idx in range(length):
        if idx % 100 == 0:
            weight = np.array(weightlist[idx])
            Y = -(weight[0] + X * weight[1]) / weight[2]
            plt.plot(X, Y)
            plt.annotate('hplane:' + str(idx), xy=(X[0], Y[0]))
    plt.show()

    print('6. 应用模型到测试数据中')
    testdata = np.mat([-0.147324, 2.874846])           # 测试数据
    m, n = testdata.shape
    testmat = np.zeros((m, n+1))
    testmat[:, 0] = 1
    testmat[:, 1:] = testdata
    result = sum(testmat * (np.mat(weights)))
    if result < 0.5:
        print(0)
    else:
        print(1)

训练结果如下：

【参考文献】

《机器学习》Mitshell，第四章

《机器学习算法原理与编程实践》郑捷，第五章5.2.2