机器学习算法推导--矩阵求导中为何会有“转置”?
之前学习神经网络推导的时候,发现在有的求导上最后结果需要转置,而有的不需要,很困惑:
浅层神经网络反向传播的困惑
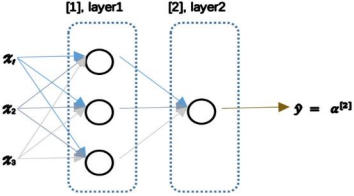
正向传播:
反向传播:

这里为什么要对W进行转置操作?为什么别处有的地方就没有转置操作?
矩阵求导知识
思来想去,突然发现自己对矩阵求导似乎一无所知,遂有:
博主第一次参考的博客 https://blog.csdn.net/u010976453/article/details/54381248 --
结果:建议大家先看评论-_- : 太感谢评论了,有了你们先趟过这潭水,让我真的少走了很多弯路,感谢。
在评论里发现的宝藏:
https://blog.csdn.net/xidianliutingting/article/details/51673207
以及在这篇博客的评论里再次发现的宝藏:
https://blog.csdn.net/shouhuxianjian/article/details/46669365
接下来就是博主的总结了:
1、矩阵微积分符号表示的两个派别:
之前会发现在有的求导上最后结果需要转置,而有的不需要,很困惑,然后才发现了这个维基上面的解释(这才是写该博文的主要价值,注意到不同的布局问题,其他部分只是为了完整性而写的),而且下面也有很多很不错的参考链接,其中就有之前的矩阵计算(2)和矩阵计算(3)的链接。维基最后更新时间:17 April 2015, at 21:34.
在数学上, 矩阵微积分是用来表示多变量的微积分,当然主要还是在矩阵空间上的。它覆盖了单一函数(单元)关于多变量的偏导,多变量函数(多元函数)关于单一变量、向量和矩阵的偏导(向量、矩阵可以被视为单一实体对待)。这种符号化的数学表示大大的简化了很多操作,例如查找多变量函数的最大值或者最小值,以及微分方程的求解系统等等。值得注意的是:下面使用的符号是在统计和工程领域中常用的,不过张量的指数表示(tensor index notation)是来自物理学。
不过有个我们之前未注意的是,有两派人它们使用着自己的符号约定,从而将矩阵微积分划分成了两个派别。这两个派别很容易区分,只要看它们写一个标量关于一个向量的导数是写成列向量还是行向量。不过这两个约定都是被大家所接受的,就算是在涉及到一般的矩阵计算的时候,将常规的向量默认视为列向量(而不是行向量)的情况下还是成立的。在矩阵微积分中,如果采取了一个约定,那么就使用该约定贯穿整个领域(例如:计量经济学,统计学,评估理论(etimation theory)和机器学习),不要混用不然会造成混乱。然而,在一个具体的领域中,不同的作者还是会使用不同的约定,因为会有来自不同派别的作者会将他们自己的约定作为标准。所以在没有去仔细的验证不同作者的资料的时候盲目的将他们的结论放在一起会有严重的错误。因而在一个完整的资料上需要确保符号的一致性。在下面的布局约定部分会有两种约定的定义介绍和比较。
————————————————
原文链接:https://blog.csdn.net/shouhuxianjian/article/details/46669365
所以会有:https://blog.csdn.net/daaikuaichuan/article/details/80620518

2、矩阵求导的基础知识:



3、豁然开朗:

全连接层反向传播矩阵推导
原文:https://blog.csdn.net/wp_csdn/article/details/79920764




