Summary
今天的比赛60+100+100=260分,没有想到第一题正解是搜索,我与AK差一段距离,这段距离,叫倒着搜。总的来说不是很难。
Problem
T1 天平
题目大意
给你N个排序好的砝码的质量,从第三个砝码开始,它的重量最少是前两个砝码的质量之和。天平容不得超过C质量的质量。问最大的质量可以是多少。
想法
一般Usaco的题目都不会水到哪里去,但是今天的。。。
有两种方法。
(1) 爆搜+剪枝
爆搜应该都会,参数是枚举到第K个,当前砝码是重S
优化一:如果当前的砝码质量加上没有抉择(没有递归到)的砝码质量还是不能比当前得出的最大值大,则剪枝
优化二:倒着搜可以减少之后的分支,当然可以降低时间复杂度,是个很了得的东西,有道题靶形数独同样适用这种方法。
(2) 中途相遇法
这个方法效率很玄,但是总比爆搜稳妥
可以把1~(n+1)/2和(n+1)/2~n这两段的方案数用dfs求出来,然后枚举。
可以用二分来找,最好用两个指针。
T2 游历的路线
题目大意
在从1城市开开始走到n城市,期间有m天,其中第m天一定要在n城市,两两城市之间来或往的马车费用是周期性的,并且有些时候可能不可以从某个城市去另一个城市,问满足条件的最小费用。
想法
显然可以用动态规划。
设f[i,j]表示第i天到第j城市
显然需要知道i-1天在哪个城市,我们可以枚举,设i-1天在k城市
f[i,j]=min{f[i-1,k]+s}(其中s代表费用,费用的周期可以用除法原理来算(x-1) mod y+1)
初始化显然,效率显然,答案显然。
T3 最短路(shortest)
题目大意
求从(0,0)~(n,m)经过点的和的最小值。
第(x,y)点的权值为f[x,y],他的计算方法是f[x,y]=f[x-1,y]+f[x,y-1],如果(x=0) or (y=0)那么f[x,y]的值为1
想法
通过一系列的对拍,我们可以发现,如下图红边的走法,必定最优,但不知道怎么证明。我们设较短边的长为n,较长边的长为m
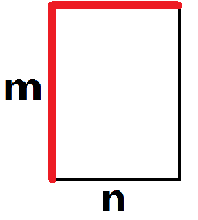
我们可以总结成一个公式
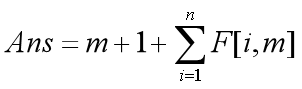
那么,关键就成了如何求出F[i,m] (i=1~n)。
我们考虑把他转化成组合数的形式
根据题目给出的F数组计算方法,可以得出f[x,y]=C(min(x,y),x+y)
那么显然F[i,m] (i=1~n)就是C(i,i+m) (i=1~n)
其实每个组合数,可以理解成一个数除另一个数,比如对于C(n,m)
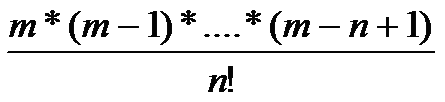
试想一下,如果x<y,求C(x,y)+C(x+1,y+1)+C(x+2,y+2),我们设上面这个式子分子为tot1,分母为tot2
C(x+1,y+1)相比C(x,y)的tot1和tot2,发现tot1多乘了y+1,tot2多乘了x+1,
C(x+2,y+2)相比C(x+1,y+1)的tot1和tot2,发现tot1多乘了y+2,tot2多乘了x+2
说明,我们每次循环,tot1都乘i+m,tot2都乘i,那么,每次的C(i,i+m)就是tot1/tot2
但是问题来了,tot1和tot2都很大,如果相除是不太可能的,先mod再除答案是错误的,只能使用逆元了。
逆元
根据费马小定理可以得到如下式子
![]()
两边同时除b得到,高斯研究过,发现是等价的
![]()
两边同时除b得到,高斯研究过,发现是等价的

两边同时乘一个a,并且交换位置,得到如下式子
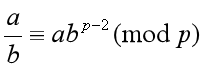
发现,我们要求a除b取模p的结果,其实是等价于abp-2取模p的结果的,也就是说,欲想知道a除b取模p的结果,其实就是算出abp-2取模p的结果就行了
因为a*b mod p,是等价于a mod p*b mod p的,ak mod p是等价于(a mod p)k的,所以我们这里可以取mod来避免高精度。
当然,F[i,m] (i=1~n)这一部分,可以使用一个组合公式就可以了,具体实现和题解请选手自行考虑。