原文地址:https://www.cnblogs.com/hanruyun/p/9620029.html
作者:子谦。
嗯,这玩意看着很难对吧,之前我还是这样想的。。直到看到了斐波那契公约数这道题
这道题一看我这种辣鸡就不会做啊,然后rqy告诉我这是傻逼题啊,我忽然就想起了以前听说过的矩阵乘。。然后懒惰的DDOSvoid大佬告诉我要做这道题,得先做斐波那契数列,要做斐波那契数列,得先做矩阵加速,要做矩阵加速,得先做矩阵快速幂。。于是,一个上午就这么过去了
回归正题
定义
什么是矩阵运算呢?
在理解这个问题前,我们先要知道什么是矩阵
百度百科给的定义如下
矩阵是一个按照长方阵列排列的复数或实数集合
复数实数什么的我们先不管,总之,矩阵就是一堆数,按照矩形排列形成的集合
那么,我们所需要记录的也就是它的长、宽以及矩阵中存储的元素
特殊的,长宽相等的矩阵我们定义它为方阵
当两个矩阵的长宽相等时,我们认为这两个矩阵为同型矩形
若矩阵为方阵,且对角线上的元素为1,其余均为0,则我们定义它为单位矩形,一个矩形与单位矩形相乘仍为原矩形
基本运算
矩阵的运算我们可以类比实数的运算来理解
在实数运算中,一般由进行运算的实数和运算符组成,运算符决定了运算类型
那么同样的,矩阵运算也是如此
加法运算
首先,我们来看加法运算
两个矩阵进行一般的加法运算的前提是两个矩阵为同型矩阵
我们只需要将对应位置的元素相加即可,如下图
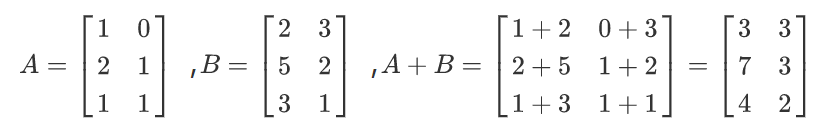
在矩阵的加法运算中,满足交换律和结合律,也就是
也许有人想问了,如果我想让两个非同型矩形进行相加可不可以实现呢?
答案是可以的,这种运算是被支持的,我们称这种运算为直和
但由于这种运算使用较少,且与本文关系不大,我们在此不多做解释,感兴趣的朋友可以阅览下面的链接,相信它会给你一个满意的答复
减法运算
在实数运算中,减法为加法的逆运算,同样的,在矩阵运算中也是如此,如下图

数乘
在实数运算中我们并没有数乘这种运算(毕竟本身就是数,直接叫乘法了)
所以在数乘运算中,我们类比向量来进行理解
在数乘向量运算中,只需要将向量中的每个元素乘上那个数就可以了
数乘矩阵也是如此,如图
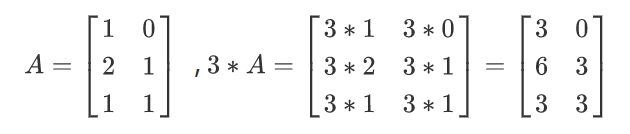
数乘矩阵运算中,满足如下运算律
矩阵乘法(矩阵乘矩阵)
在向量乘向量的运算中,是将每个元素与它对应的元素相乘,求所有乘积之和
那么矩阵乘矩阵是不是就是两个同型矩阵的对应元素相乘呢?
图样图森破
两个矩阵相乘的前提是前一个矩阵的列数等于后一个矩阵的行数
举个栗子,为矩阵,为矩阵,为矩阵,那么可以与相乘,可以与相乘,可以与相乘,其他均不成立
我们知道了什么情况下两个矩阵可以相乘,那么他们怎么相乘呢?不讲每个对应位置相乘还能怎么乘呢?
设为矩阵,为矩阵,那么它们的乘积则为一个矩阵
是不是不太好理解,没关系看看图就知道了
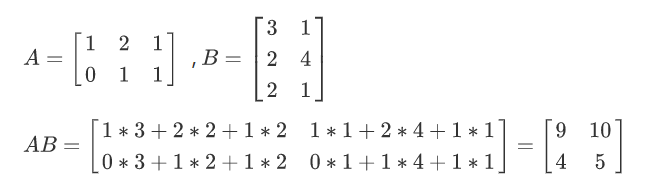
在矩阵乘法中满足以下运算律:
在普通的乘法中,一个数乘1还是等于它本身,在矩阵乘法中也有这么一个“1”,它就是单位矩阵
不同于普通乘法中的单位1,对于不同矩阵他们的单位矩阵大小是不同的
对于的矩阵,它的单位矩阵大小为,对于的矩阵,它的单位矩阵大小为
也就是说单位矩阵都是正方形的,这是因为只有正方形的矩阵能保证结果和前一个矩阵形状相同
单位矩阵的元素非0即1,从左上角到右下角的对角线上元素皆为1,其他皆为0