【题目背景】
小G 同学总是在树上走路。小S 看不下去了,决定阻止小G 同学。
【题目描述】
有一棵 n 个点的树,树上有 m 条路径,每条路径为 x[i]到y[i] 的树上最短路径(不经过相同的边),小 S 想要摧毁树上的 K 个点, 使得每一条路径上都有至少一个点被摧毁。
你只需要求出最小的K,而不用输出摧毁了哪些点。
| 数据点编号 | n<= | m<= |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 100 | 15 |
| 3 | 100 | 15 |
| 4 | 100 | 100 |
| 5 | 1000 | 1000 |
| 6 | 5000 | 5000 |
| 7 | 5000 | 5000 |
| 8 | 100000 | 100000 |
| 9 | 100000 | 100000 |
| 10 | 100000 | 100000 |
【样例输入】
5 2
1 2
2 3
2 4
2 5
1 5
3 4
【样例输出】
1
【提示】
如果需要用到较大的栈空间。
可以在编译命令加上-Wl,--stack=2333333333。评测时开栈。
题解
受洛谷P1967 货车运输启发,这题很像LCA。
于是我们就尝试切LCA。
首先,不难发现阻断LCA是可行的,那么是最优的吗?
对于一颗子树内的点,如果从该子树的点要延伸出子树外,那必须经过最顶端的点。
如图,对于一个点,若要与外面有联系,那必定要经过(lca(a,b))。
那两点的联系在子树内呢?如果是(c o d),那显然是无关的,那(e o b)呢?我们发现最优应该切(lca(e, b))。
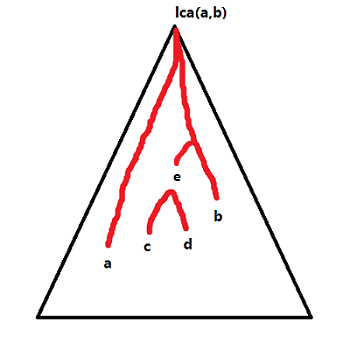
那不是就WA了吗?不。我们发现:如果我们先切(lca(e, b)),到(a o b)是特判一下即可。
由于数据很水,判是否联通用暴力爬就可以了。
下面上代码,刚学树剖,于是就打了个树剖。
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 100005;
struct Edge
{
int to, nxt;
} e[maxn<<1];
int first[maxn];
int nowm;
inline void add_edge(int from, int to)
{
e[++nowm].nxt = first[from];
e[nowm].to = to;
first[from] = nowm;
e[++nowm].nxt = first[to];
e[nowm].to = from;
first[to] = nowm;
}
int fa[maxn], son[maxn], dep[maxn], val[maxn];
inline void dfs1(int x)//找重链,标记深度与父亲
{
dep[x] = dep[fa[x]] + 1;
val[x] = 1;
for(int i = first[x], dd; i; i = e[i].nxt)
{
dd = e[i].to;
if(dd == fa[x])
continue;
fa[dd] = x;
dfs1(dd);
val[x] += val[dd];
if(!son[x] || val[dd] > val[son[x]])
son[x] = dd;
}
}
int top[maxn];
inline void dfs2(int x, int ff)//寻找重链的顶端
{
top[x] = ff;
if(son[x])
dfs2(son[x], ff);
for(int i = first[x], dd; i; i = e[i].nxt)
{
dd = e[i].to;
if(dd != fa[x] && dd != son[x])
dfs2(dd, dd);
}
}
inline void init(int s)
{
dfs1(s);
dfs2(s, s);
}
inline int lca(int a, int b)
{
while(top[a] != top[b])
{
if(dep[top[a]] >= dep[top[b]])
a = fa[top[a]];
else
b = fa[top[b]];
}
return dep[a] < dep[b] ? a : b;
}
struct sxd
{
int a, b, t;
inline bool operator < (const sxd& other) const
{
return dep[t] > dep[other.t];
}
} ask[maxn];
bool biao[maxn];
inline bool pan(int a, int b)
{
for(; a != fa[b]; a = fa[a])
if(biao[a])
return true;
return false;
}
int main()
{
freopen("walk.in", "r", stdin);
freopen("walk.out", "w", stdout);
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1, f, t; i < n; ++i)
{
scanf("%d%d", &f, &t);
add_edge(f, t);
}
init(1);
for(int i = 1; i <= m; ++i)
{
scanf("%d%d", &ask[i].a, &ask[i].b);
ask[i].t = lca(ask[i].a, ask[i].b);//树剖lca模板
}
sort(ask+1, ask+m+1);//将提问排序,从下往上阻断
int ans = 0;
for(int i = 1; i <= m; ++i)//暴力往上爬……(竟不会T,还是最优解)
{
if(pan(ask[i].a, ask[i].t) || pan(ask[i].b, ask[i].t))
continue;
ans++;
biao[ask[i].t] = true;
}
printf("%d
", ans);
return 0;
}