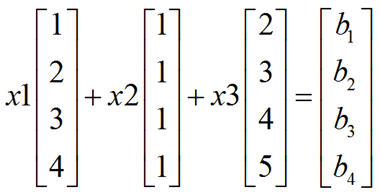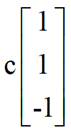线性代数(笔记六)
课程来源:网易云课堂学习计划(课程链接)
作者简述:作者为一名正在读研的学生,自己的数学状态较差。本科期间所学均能算跟得上,而且通过自己的努力经过了研究生考试。但是对数学的理解并不透彻,只是根据课上所学去做题而已。如今科研中,许多过程均需要用到所学的数学知识,然而一个好的理解和一个扎实的基础才是科研之本。数学虽然是作为一种工具,如果不了解含义,无论是是使用上还是在其基础之上进行修改均显得支支吾吾。于是决定重新学习线性代数相关知识,并做此笔记以供复习或和他人分享。
用途:此系列文章均是作者在课上所学及其自己相关的数学思想所做的笔记,如有理解错误之处还望大家指出。本系列文章均可不咨询情况下任意转载和学习(不可商用)。
作者研究方向为机器学习,如果有相同方向的小伙伴想一起学习,请加QQ123854340(备注来源博客),如果人数较多还可能建群。同时发现文章中有错误之处也请发邮件到123854340@qq.com。
在上节课中,我们主要介绍了矩阵的转置和置换,在这节课中我们将讲述向量空间、及子空间等相关知识。
一、向量空间(vector space)
首先要讨论的问题就是什么是向量空间,即向量空间的定义。首先我们给出一个例子,二维空间中所有的向量(向量的分量用实数表示)。那么,由这些向量构成的集合所形成的就是一个二维向量空间(R2)。在这里它满足,任意向量的数乘、相加、数乘和相加的组合所得的向量均在其内部。
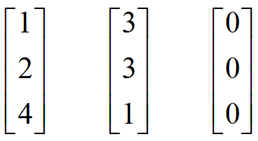
下面列举两个非向量空间的例子,如图:
在上面图1中,我们可以看到当我们尝试用-1和其中某个向量(除零向量)相乘时,其所得的向量一定不在第一象限中。所以,他不是向量空间。图2中是R2中不含有0向量,那么当我们取一个向量和一个向量的反向向量相加时((2,3),(-2,-3))所得到的零向量也不在其内部,故其也不是向量空间。
综上所述,我们对向量空间有如下定义:Vector space requirements v+w and cv are in the sapce all combs cv+dw are in the space(这是教授给的)。如果一个向量集合所组成的空间满足两种操作(数乘、相加)且通过这两种操作及他们之间的线性组合后的向量仍然在这个集合所形成的空间中。那么我们就称它为向量空间。
二、子空间(subspace)
对于子空间,一个很好的解释就是它满足向量空间的规则,又不包含向量空间中所有的向量。例如在R2中的一条过原点的直线即为R2的子空间。如图:
下面让我们去列举下在R2(二维向量空间)和R3(三维向量空间)中的所有的子空间。
R2中的子空间有:
①R2本身
②任何一条过原点(0,0)的直线(它就像R1一样,却不同于R1)
③零向量
R3中的子空间有:
①R3本身
②任何一个过原点(0,0,0)的平面
③任何一条过原点(0,0,0)的直线。
④零向量
以上列举了R2和R3中所有的子空间,我们可以根据这些去思考Rn中的子空间是以什么样的形式的存在,方便以后的理解。
我们用P表示通过原点的平面,用L表示通过原点的直线。那么他们均是R3中的子空间,试问(P∩L)、(P∪L)是否还是子空间呢?从直观的角度考虑,显然P∩L仍然是子空间,而P∪L则不是。
由此在课中给出,向量空间中的子空间S、T,他们的交(S∩T)任然是一个子空间!
三、矩阵的列空间(column space)
列空间是由一个矩阵所构造的子空间,下面我们给出一个矩阵A,如图:
矩阵A的所包含的列有(不包含如下0向量):
当矩阵的列及零向量自由组合即可形成一个子空间,这个子空间是经过原点的平面,他们是三维向量空间的子空间(矩阵的列向量为三维向量空间中的两个向量)
下面我们看如下一个例子:
有上述知识我们可知,矩阵A的列空间是由矩阵A的列的线性组合而形成的,那么问题是这个空间具体什么样?我们怎么表示他呢?
于是,我们把求解方程组Ax = b与其相结合。首先,我们要了解的问题是,对于任意的b,方程组总是有解么?答案很显然是否定的!矩阵A可以看成是三个列向量,而x则可以看成是向量。博文前几章讲过,我们可以把矩阵和向量的乘积看作是矩阵列向量通过x各分量的线性组合。即:
显然,这是四维空间向量中的三个向量的线性组合,假设他们均为线性无关,那么他们的组合也无法布满整个四维空间(至少需要四个线性无关向量)。此时,我们可以得出矩阵A的列向量线性组合后所形成的空间为R4的子空间。那么对于任意的b则可能无法表示,所以方程组可能是无解的。那么什么样的b使得其有解呢?很显然的就是b必须在其所构成的子空间内部,才能有解。例如如下b:
四、矩阵的零空间(null space)
对于一个矩阵,它的零空间为Ax = 0的所有的解所构成的向量空间。很显然x是三维的,所以其解空间也是三维的。对于Ax = 0:
我们能很容易看出他的解有(我们还没讲到对Ax=0的求解,但这个例子很简单就能看出):
我们将解进一步表示为:
由这个解我们可以看出,它是三维空间中一条过原点的直线。
不同于列空间,列空间是由其列向量构造而成,其一定满足向量空间的规则。那么对于零空间,我们给出如下证明。
如果Av = 0 且 Aw = 0 那么 A(v+w)= Av+Aw = 0
同理,如果Av = 0 那么 A(cv) = c(Av)= 0(c为常数)