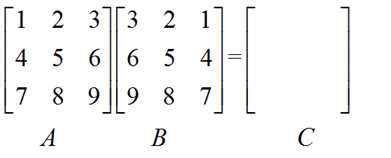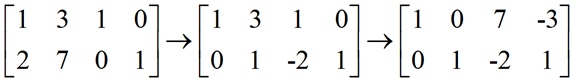线性代数(笔记三)
课程来源:网易云课堂学习计划(课程链接)
作者简述:作者为一名正在读研的学生,自己的数学状态较差。本科期间所学均能算跟得上,而且通过自己的努力经过了研究生考试。但是对数学的理解并不透彻,只是根据课上所学去做题而已。如今科研中,许多过程均需要用到所学的数学知识,然而一个好的理解和一个扎实的基础才是科研之本。数学虽然是作为一种工具,如果不了解含义,无论是是使用上还是在其基础之上进行修改均显得支支吾吾。于是决定重新学习线性代数相关知识,并做此笔记以供复习或和他人分享。
用途:此系列文章均是作者在课上所学及其自己相关的数学思想所做的笔记,如有理解错误之处还望大家指出。本系列文章均可不咨询情况下任意转载和学习(不可商用)。
作者研究方向为机器学习,如果有相同方向的小伙伴想一起学习,请加QQ123854340(备注来源博客),如果人数较多还可能建群。同时发现文章中有错误之处也请发邮件到123854340@qq.com。
在上节课中,我们说了两种形式的消元。在矩阵形式的消元中,我们利用一个矩阵左乘另外一个用来行变换的矩阵而进行消元。所以在矩阵本身的理解中,可以看做是对线性空间中的一种变换。这节课,我们来说一下矩阵之间的乘法和矩阵的逆。
一、矩阵的乘法
这里所说的矩阵的乘法是指矩阵和矩阵相乘。根据课中教授所述,矩阵乘法有五种方法,下面我们就来看看这五种方法。
1、第一种为常规的算法(这个大家都很熟悉,我们书中定义的求解方法。)具体如下:
如图 c32 = a31*b21+a32*b22+a33*b23;类似的,求C中任何一个元素,都由该元素所在行对应的A的行向量和其所在列对应的B的列向量的乘积而得。
2、第二种在上节中已经有所引用,就是将矩阵与矩阵相乘看做是矩阵列的线性组合,其中一个矩阵为系数矩阵。具体如下:
对于这个矩阵相乘AB = C,我们可以将B看做为系数矩阵,将A的各个列通过B中对应的系数进行线性组合,即如下步骤:
A的列线性组合中的系数使用到的是B中的第一列,所以求得的结果为C中的第一列。类似的我们可以换B的第二列而求解C的第二列。(这里和之前讲过的矩阵和列向量的乘积求解过程相似)
3、第三种在上节中也已经有所引用,就是将矩阵与矩阵相乘看做是矩阵行的线性组合,其中一个矩阵为系数矩阵。具体如下:
整个过程类似于方法二,将矩阵A的行看做线性组合的系数,将矩阵B的行对应系数进行线性组合即可获得对应行的结果。
4、第四种为第一种对称的方法,第一种用A的行乘B的列,而这里用的是A的列和B的行进行相乘。求出所有的矩阵后再相加。这种方法不太常用,可以看看有助于理解。具体如下:
利用A的第一列和B的第一行可求出一个矩阵C1,同样的可利用第二、第三列和第二、第三行来求解C2、C3,然后C = C1 + C2 + C3。
5、第五种为分块相乘,这种方法一般不太常用,但对于有规律的矩阵或者矩阵很大的情况下可以考虑用这种方法,这样会非常容易求解。
对于如上两个矩阵相乘,我们可以先给这两个矩阵按照一定的特征分块。第一个矩阵分为A1到A4,第二块分为B1到B4。两个矩阵分块后相乘也准守矩阵乘法的规则,这里我们用的是第一种方法进行相乘。(其中每个块也是矩阵,只是规模减少了。当分块中矩阵比较有特点,则求解很容易。)
二、矩阵的逆
对于AB = C,由上节矩阵形式的消元可知,可以将A看做是B变成C的一种变换,即B所做的行变换均叠加在A中。然而,我们也讨论了如果将C变回B,我们需要的是将所有对B的变换,逆向的作用于C上。比如我对B第一行都乘了3,那么变回的过程就把C第一行乘1/3就可以变回去了。此时所谓的逆变换就是A的逆(这里用A~表示),那么很显然就可知道如果A和A的逆A~都作用于B,矩阵B是不变的。即A*A~ = I(I为单位矩阵)。
上面的表达式可以看做为矩阵逆的定义,我大致说了下它得来的思路。类似的A~*A = I。但是并不是所有的A都有逆矩阵。比如如下矩阵:
这个A就没有逆矩阵,因为无法找到一个矩阵A~和他相乘得I。那么为什么呢?我的理解是这样的,我们可以借助于矩阵乘法中的第二种方法。存在一个系数矩阵B和A相乘(A*B),相当于A的列的线性组合,那么很明显的问题是A的两个列对应成比例,则其线性组合后也处在同一条直线上,而不能布满整个面(第一节中有说)。这是从一个角度进行理解的,书中对于存不存在逆还是有很好的方法的(行列式方法)。
课中给了一个方法是如果你能找到一个非零向量X满足AX = 0则,A就是没有逆的。具体证明如下:
首先假设A存在逆A~,那么A*A~ = I = A~*A。对于AX = 0,左右两边左乘矩阵A~,可得A~*AX = 0,则X = 0。但是我们的X是非0向量,所以矛盾,则可证明A为不可逆的。
三、矩阵的逆的求解
当我们想获得A的矩阵的逆的时候,我们会试图用定义写出如下表达式:
通过这个表达式去求解a、b、c、d,从而获得逆。在这个表达式中求解系数,也不是很容易。它等价于求解两个方程组。如下:
这里课中介绍了一种方法是Gauss-Jordan消元法,同时在构造的增广矩阵中对两个方程进行消元。构造的增广矩阵及消元变换如下:
第二步到第三步是利用第二行进行向上消元,用第一行减去第二行的三倍。我们的目的是将左侧矩阵变为I,那么我们右侧获得的就是矩阵A的逆A~。原因如下:
我们对这个增广矩阵做变换E,即E[A I] = [I B]。最后将左侧A变为了I,那么为什么B(右侧)为A的逆?由表达式可知,E A = I,那么由矩阵逆的定义A*A~ = I可知,E为A~。又因为E I = B ,则B = E。