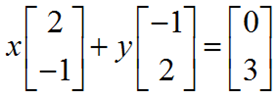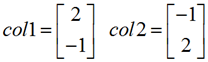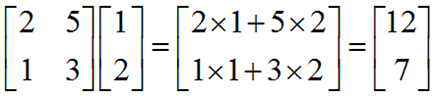线性代数(笔记一)
课程来源:网易云课堂学习计划(课程链接)
作者简述:作者为一名正在读研的学生,自己的数学状态较差。本科期间所学均能算跟得上,而且通过自己的努力经过了研究生考试。但是对数学的理解并不透彻,只是根据课上所学去做题而已。如今科研中,许多过程均需要用到所学的数学知识,然而一个好的理解和一个扎实的基础才是科研之本。数学虽然是作为一种工具,如果不了解含义,无论是是使用上还是在其基础之上进行修改均显得支支吾吾。于是决定重新学习线性代数相关知识,并做此笔记以供复习或和他人分享。
用途:此系列文章均是作者在课上所学及其自己相关的数学思想所做的笔记,如有理解错误之处还望大家指出。本系列文章均可不咨询情况下任意转载和学习(不可商用)。
作者研究方向为机器学习,如果有相同方向的小伙伴想一起学习,请加QQ123854340(备注来源博客),如果人数较多还可能建群。同时发现文章中有错误之处也请发邮件到123854340@qq.com。
方程组的几何解释:
在第一节课中讲述的是线性代数的引入,课程中的教授认为方程组是引入线性代数最好的开端。下面来看如下方程组:
用矩阵和向量乘积所表示的形式为:Ax = b
如果以行(row)的形式进行展开的话,则在二维空间中每一行所表示的即为一条直线。则其意义为求两条直线的交点,这个交点也就是方程组的解(这也是我们很熟知的)。
如果以列(column)的形式进行展开的话,则可写成如下格式:
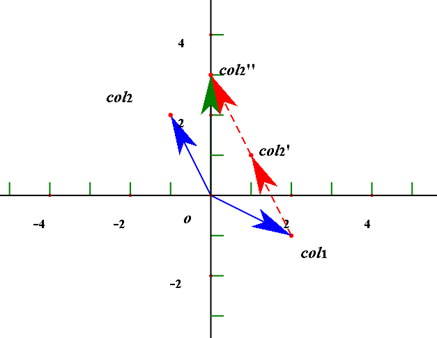
在这个表示的过程中,我们可以发现col1是一个向量,col2也是一个向量。则此方程组又可理解为两个向量的组合(combination)。
那么思考如下问题:根据这个线性组合,如果x,y选取所有可选的值,形成了所有的组合,那么结果会如何?(当然对应这两个向量col1,col2而言,他们的组合将会布满整个坐标系)这样很容易就将向量的线性组合和方程组求解的问题联系到了一起。对于任意的b都可以求解出对应的x,y的值。接下来看一下三维的例子。
给出如下方程组:

用矩阵和向量乘积所表示的形式为:Ax = b
如果以行(row)的形式进行展开的话,则在三维空间中每一行所表示的即为一一个平面。则其意义为求三个平面的交点,这个交点也就是方程组的解。图过于复杂就不画了。
而对应其以列(column)的形式进行展开的话,则可以写成如下格式:
其所表示的意义为三个向量的线性组合。那么对应于三维中所要思考的问题就是,这三个向量的所有的组合是否可以布满整个三维空间呢?很显然对于这个例子来说答案是肯定的。但是如果三个向量共面则答案是否定的(这里只说了一种情况)。
矩阵与向量乘积的运算:
对于如上两种形式的展开(row column),在计算矩阵与向量乘积的运算过程中,也对应着两种方法。
1.以线性组合的方式进行运算(在矩阵较小时比较推荐,在使用中经常被忽略的一种方式)
2.以方程形式进行运算(常规的矩阵乘法)
以上就是第一节课所有的内容,例子虽然很简单,却表明了其中的含义,并将线性代数引入。