C笔记01-C简介与补码

文章目录

• 计算机及程序语言发展
• 计算机中数的存储
• 补充知识:补码的原理

所学视频及PPT截图来源:爱课程资源共享课

计算机及程序语言发展

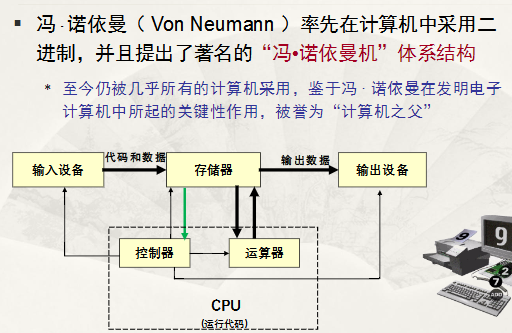
0.计算机的体系结构

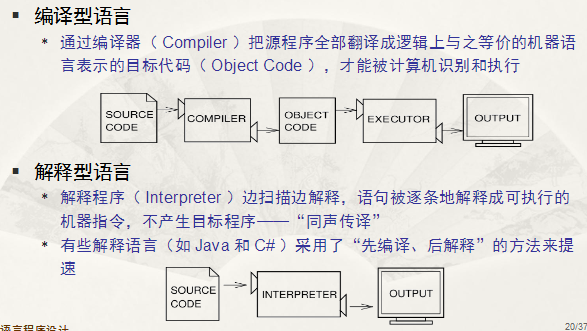
1.计算机语言的发展历程

• 机器码阶段
  

• 汇编阶段
  

• 高级语言阶段
  

2.高级语言

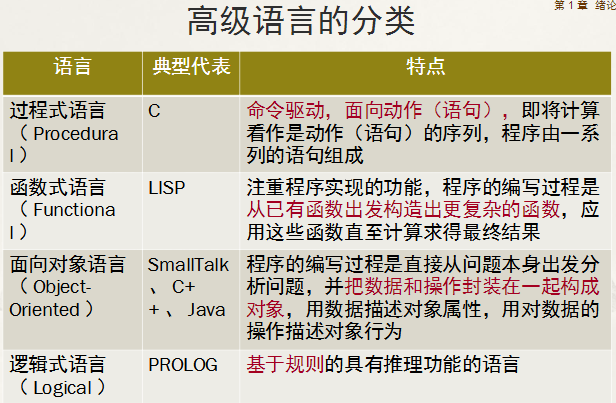
• 高级语言分类
  
  

3.C语言标准

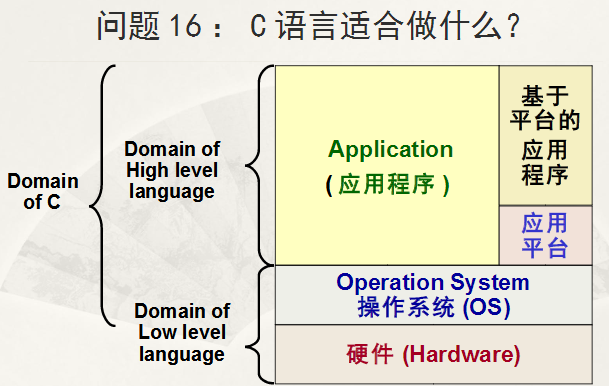
4.C语言的应用

---

计算机中数的存储

人类自然认知的数:十进制数
计算机中存储的数:二进制(硬件上好实现)

1.二进制数

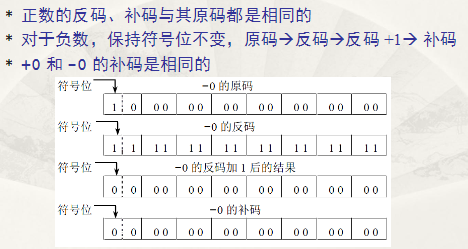
2.正负数的二进制表示与双零问题

3.补码的引入

• 双零问题的解决
  

---

补充知识:补码的原理

1.怎么看待"运算"?

计算机的视角:0/1序列的逻辑运算.没有什么无符号或有符号的概念和区别,也没有什么加减乘除法的概念,一切都是0/1序列,一切操作都是逻辑运算而已.
人类的视角:用逻辑电路对计算进行判断和控制,使得它表现出我们想要或我们能理解的内涵与信息.
由此,引申出两个概念:

• 机器数:从计算机的角度看待的一个值
• 真值:机器数所表示的内涵与信息,从人类角度看待的一个值
  举例:-6在计算机中的表示码为11010(假设计算机用于表示数的位数为5位)
  机器数:1×2⁴+1×2³+0×2²+1×2¹+0×2⁰=26
  真值:最高位为符号位,是个负数.剩余码1010,进行反补码的操作,得到0110,化为十进制为-6

2.源码,反码,补码的机器数与真值

3.补码的优势

• 解决了双零问题
• 符号位可以参与运算,大大简化了硬件电路的实现

4.定点补码计算法则及其证明(为什么可以用补码表示数和进行计算)
计算法则 : 在不溢出情况下, [X]补+[Y]补=[X+Y]补 (溢出:结果超出编码所能表示的数的范围)
设计算机补码的位数为M.且x=|X|,y=|Y|

溢出的情况:
0 < x <2^M-1
0 < y <2^M-1
两正相加时: x+y >= 2^M-1(两正相加,向符号位进位)
两负相加时: x+y >2^M-1(两负相加,非符号位之和不足以向符号位进位)

(1)情况1:两正数相加正向溢出
(2)情况2:两负数相加反向溢出

不溢出的情况:
0 < x <= 2^M-1
0 < y <= 2^M-1
两正相加时: x+y < 2^M-1(两正相加,不向符号位进位)
两负相加时: x+y >= 2^M-1(两负相加,非符号位之和足以向符号位进位)

(3)情况3:正数相加不溢出
等式左边:
[X]补+[Y]补=x+y
等式右边:
[X+Y]补=x+y
左边等于右边,等式成立

(3)情况4:负数相不溢出
等式左边:
[X]补+[Y]补=2^M+2^M-(x+y)
(注:第一个2^M是负数符号位相加的天然进位,可以舍去),所以左边的最终结果为: 2^M-(x+y)
等式右边:
[X+Y]补=2^M-(x+y)
左边等于右边,等式成立

(4)正负相加绝不会溢出
0 < x <= 2^M-1
0 < y <= 2^M-1
则根据不等式,可推出:
-2^M-1 < x-y < 2^M-1,即: 0 <= |x-y| < 2^M-1.
因此,正负数相加的结果也可以被表示,绝不会溢出.

我们假设X为正,Y为负:
等式左边:
[X]补+[Y]补 = x+2^M-y = 2^M-(y-x) = 2^M+(x-y)
当x>=y时,左边 = 2^M+(x-y) = x-y(注:2^M相当于符号位向更高位的进位,而符号位本身就是最高位,故可以舍去)
当x<y时,左边 = 2^M+(x-y) = 2^M-(y-x)
等式右边:
当X+Y>=0时,x>=y,[X+Y]补= x-y
当X+Y<0时,x<y,[X+Y]补= 2^M-(y-x)
左边等于右边,等式成立
(5)两操作数之中至少有一个为0的情况: 显然,等式是成立的.

综上所述: 在不溢出的情况下,[X]补+[Y]补=[X+Y]补成立.

5.补码运算原理

• 化减法为加法的原理: (钟表模型)
  

• 最高位参与运算的原理:
  (1)非负数相加,不溢出的情况下,最高位均为0,相加亦为0.
  (2)两负数相加,最高位均为1,相加进位变为0;而在不溢出的情况下,两负数的非符号部分的和会产生进位,成为新的符号位.
  (3)一正一负相加,例如: (正数X与负数Y)
  [X]补+[Y]补=x+2^M-y

  • 当x>y,也就是结果为正时,为便于理解,上式可变为 2^M+(x-y) ,其中的2^M为符号位的进位,舍去.结果即为: x-y .怎么理解呢?就是当x-y>0时,两数的非符号部分的和会向符号位进位,与符号位的1相加又会进位,使得符号位为0,代表正值.
  • 当x<y,也就是结果为负时,为便于理解,上式子可变为 2^M-(y-x) ,显然这是负数 Z=X+Y 的补码.怎么理解呢?就是当y-x>0时,两数的非符号部分的和不足以向符号位进位,所以符号位相加为1,代表负值.

6.注意事项与说明:

• 所谓的最高位(MSB),也就是符号位参与运算仅仅是指补码之间进行加法运算时而言.原码,反码,补码的码种之间的互相转换时,符号位是保持不变,不参与变换和运算的.
• 正因为上面的规定,所以关于编码10000…0000有一个问题,那就是当它作为补码时,它是没有原码或反码的.因为,在不动用符号位的情况下,它是没有办法完成减1这样的操作,也无法求得其原码与反码.一般用它来代表编码所能代表的负数的下限值.
• 对于上述的特殊补码:
  • 任何负数补码与之相加,溢出
  • 任何整数与之相加,变为负数(因为负数下限值的绝对值大于正数上限值的绝对值),但运算正确不会出错
  • 因此,上述特殊补码也是适用补码运算规则的,可以参与运算而不出错.