Binary Classification
把图像展平成一个列向量x,x作为输入得到输出y,y是一个判断是猫或不是猫的概率。

Notation used in this course
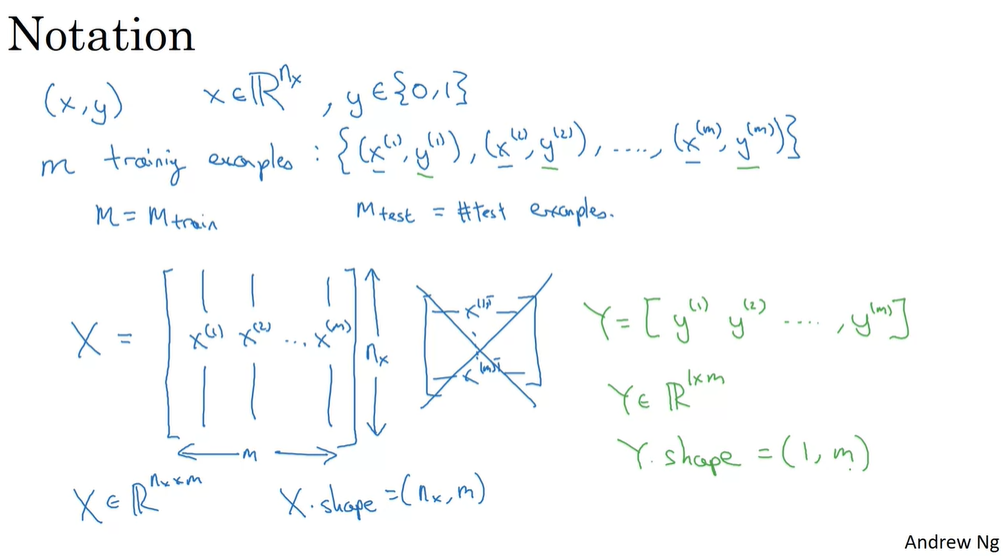
如果有m个训练样本,直观的做法可能是用for循环遍历所有的样本。但是在深度学习中应该像上图这样,把m个样本合成一个m列的向量(或矩阵),从而实现并行计算。
Logistic Regression

Sigmoid函数:(displaystyle sigma(z) = frac{1}{1+e^{-z}})
practice:

总结:
- y是概率,通过y = wx + b这种线性回归的方法无法使y的值在0~1,于是我们引入Sigmoid函数,由线性回归变成逻辑回归。
Logistic Regression Cost Function
你可以把损失函数Loss function定义成
(L(hat y,y)=frac{1}{2}(hat y-y)^2)
但在逻辑回归里一般不这么做,因为这样会使我们讨论的优化问题变成非凸的,所以优化问题会产生许多个局部最优解,梯度下降算法也无法找到全局最优解。
所以在逻辑回归中,我们使用的损失函数Loss function是:
( L(hat y,y)=-[yloghat y+(1-y)log(1-hat y)] )
直观的感受一下为什么这个函数可以作为损失函数:
( ifquad y=1:L(hat y,y)=-loghat yquad leftarrow quad want loghat y large,want hat y large\ ifquad y=0:L(hat y,y)=-log(1-hat y)quad leftarrow quad want 1-loghat y large,want hat y small )
所以代价函数Cost function为:
( displaystyle J(w,b)=frac{1}{m}sum_{i=1}^mL(hat y_i,y_i)=-frac{1}{m}sum_{i=1}^m[y_iloghat y_i+(1-y_i)log(1-hat y_i)] )

Gradient Descent
在Machine Learning(1) —— Andrew Ng里已经写过,这里不再赘述。
视频里讲解导数用了另一种直观的方法:y对x的导数就是当x改变时,y改变多少。
例如y = 3x,当x由1.0增加到1.1时,y由3.0增加到3.3,y的增量是x增量的3倍,所以y对x的导数为3.
反向传播求导要用到链式法则。y=f(x), x=g(a), a改变会引起x改变从而引起y改变,所以y对a的导数等于y对x的导数乘以x对a的导数。
Logistic Regression Gradient Descent
在逻辑回归中,我们要做的就是修改w和b来减少损失函数。
1个样本(这个样本有两个特征)的反向传播实例:

Gradient Descent on m Examples
上节介绍了一个样本的Gradient Descent,如果是m个样本,计算过程如下:

在这个例子里样本的特征数只有两个(n=2),当样本的特征数增大时,还需要一个for循环来进行处理。
你会发现, 在你的代码里有循环会降低算法的运行效率。在深度学习领域,我们会转移到一个越来越大的数据集, 因此, 能够实现您的算法, 而无需使用显式循环是非常重要的, 这将帮助您扩展到更大的数据集。而矢量化技术, 使您可以摆脱这些代码中的显式循环。这样你就可以实现这所有的代码实现一次梯度下降的迭代, 而不使用任何循环。
Vectorization

所以每当你想要写for循环的时候 先看看是否可以通过调用NumPy的内置函数来避免for循环

让我们将这些知识运用到逻辑回归的梯度下降算法实现中,看看我们是否可以至少摆脱两个for循环中的一个。这是我们计算逻辑回归中的导数的代码,这里有两个for循环,接下来我们要消灭这第二个for循环。
这就是我们要在这一页做的 我们的做法是:不再将dw_1 dw_2等显式地初始化为零,移除这一段,然后令dw成为一个向量,令dw=np.zeros((n_x,1)),即n_x乘1的向量。接着在这里,不再使用针对单个元素的for循环,而是使用这个针对向量值的运算 dw+=x(i)dz(i)。最后,不再使用这一段,而是使用dw/=m

Vectorizing Logistic Regression

摆脱第一个循环:

全部实现:

A note on python/numpy vectors
Python提供了广播操作的能力,更广泛地说,Python和NumPy带来了极佳的灵活性。我认为这既是Python作为一门编程语言的优势,也是它的劣势。其优势在于增加了语言的表达性,凭借其强大的灵活性,你只用仅仅一行代码就能完成大量的工作。但这也带来一些缺点,因为广播操作和其强大的灵活性,有时会引入十分微妙或者非常奇怪的bug,如果你并不熟悉诸如广播等特性的各种复杂的工作机制的话。例如 如果你将一个列向量与行向量相加,你可能会期望它抛出维度不匹配或者类型错误之类的报错,但实际上,你会得到一个行向量和列向量求和后的矩阵。
比如:
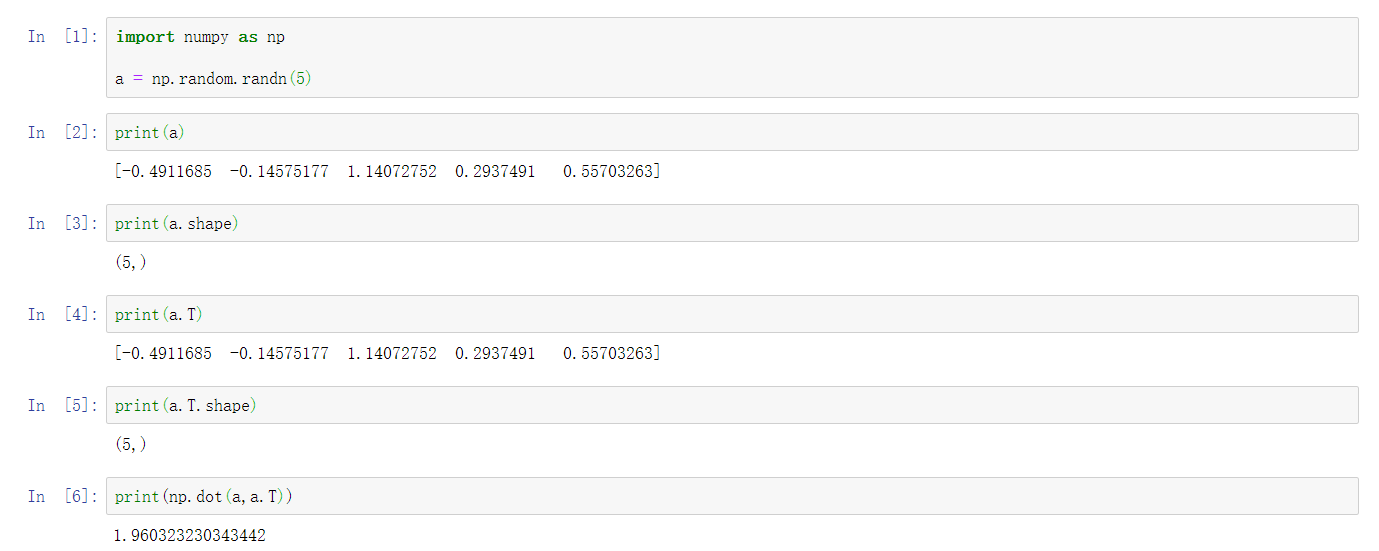
- 令a=np.random.randn(5),这会产生5个高斯随机变量并储存在数组a中。输入print(a),a的形状是这种(5,)的结构
- 这在Python中叫做秩为1的数组,它既不是行向量,也不是列向量,这会略微导致一些不直观的影响
- 比如:我打印a的转置,它的结果看上去和a一样。又如:打印a和a转置的内积,你也许认为a乘以a转置或者说a的外积是一个矩阵。但如果我这样写得到的却是一个数字
- 所以,我建议你在编写神经网络时不要使用这种数据结构,即形如(5,)或者(n,)这样的秩为1的数组。而是令a的形状为(5,1) 这会使a成为一个5乘1的列向量
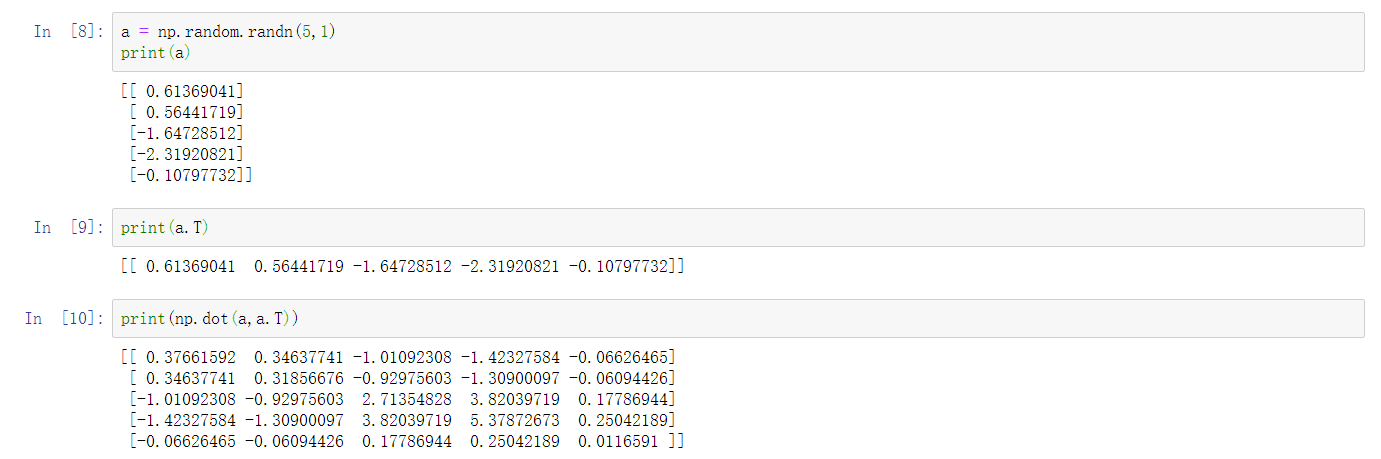
在之前a和a转置看起来是一样的,而现在a的转置是一个行向量。要注意这个细微的差别,使用这种数据结构时,打印a转置的结果中有两个方括号,而之前却只有一个方括号。
区别在于 这是一个真正的1乘5的矩阵,而之前的是秩为1的数组。并且,如果你打印a和a转置的积,这样会得到向量的外积,是一个矩阵。
这种秩为1的数组,是个很奇怪的数据结构。它的行为并不总与行向量或者列向量相一致,这使得它会带来一些不直观的影响。所以我的建议是:当你在做编程练习时,或者准确地说,在实现作业中的逻辑回归或神经网络时,不要使用这种秩1为数组。
我在编程时还经常会做这样一件事 如果我不太确定某一个向量的维度 我通常会将其放入断言语句中 就像在这里 用来确保a是5乘1的向量 所以它是个列向量 执行这些断言的成本很低 并且还能充当代码的文档
assert语句:条件为False的时候触发异常

最后 如果出于某些原因 你得到了一个秩1为数组 你可以用reshape来改变它的形状 a=a.reshape((5,1)) 比如使其成为(5,1)或者(1,5)的数组 这样它就会始终表现为列向量或者行向量。
注意:
- a.reshape((5,1))是产生一个copy,不会对原数据产生影响,一定要赋值给a,a才会发生变化。
- 如果用np.savetxt保存一个shape为(N,1)的数据,再一次从该文件使用np.loadtxt读取后,这个数据的shape会莫名其妙的变成(N,),需要用reshape把它变成shape=(N,1)。
Explanation of logistic regression cost function
损失函数在单一样本上的例子:

代价函数在整个训练样本上:

I.I.D:独立同分布(Independent and Identically Distributed)