1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define int long long
6
7 const int N = 3e5+100 ,inf = 0x3f3f3f3f;
8
9 int n,arr[N],k;
10 signed main(){
11 cin>>n>>k;
12 for(int i=1;i<=n;i++) cin>>arr[i];
13 sort(arr+1,arr+1+n);
14 int last=-inf,s=0;
15 for(int i=1;i<=n;i++){
16 if(arr[i]-last>=k){
17 last=arr[i];
18 s++;
19 }
20 }
21 cout<<s;
22 return 0;
23 }

1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define int long long
6
7 const int N = 3e5+100 ,inf = 0x3f3f3f3f;
8 int p,q;
9
10 signed main(){
11 int T=1;
12 cin>>T;
13 while(T--){
14 cin>>p>>q;
15 int B=(2*q+p)*q;
16 int x=(2*q+p);//x=a+b B=a*b==> a=x-b, b*b-xb+B=0
17 int del=x*x-4*B;
18 //cout<<del<<endl;
19 if(del<0||(del!=((int)(sqrt(del)))*((int)(sqrt(del))))){
20 cout<<"0 0"<<endl;
21 continue;
22 }
23 int sd=sqrt(del);
24 int b1=0,b2=0;
25 if((x+sd)%2){
26 b1=-1;
27 }else{
28 b1=(x+sd)/2;
29 }
30 if((x-sd)<1||(x-sd)%2){
31 b2=-1;
32 }else{
33 b2=(x-sd)/2;
34 }
35 int a1=x-b1,a2=x-b2;
36 if(a1>=1&&b1>=1){
37 int t=__gcd(a1,b1);
38 cout<<a1/t<<" "<<b1/t<<endl;
39 }else if(a2>=1&&b2>=1){
40 int t=__gcd(a2,b2);
41 cout<<a2<<" "<<b2<<endl;
42 }else{
43 cout<<"0 0"<<endl;
44 }
45 }
46 return 0;
47 }
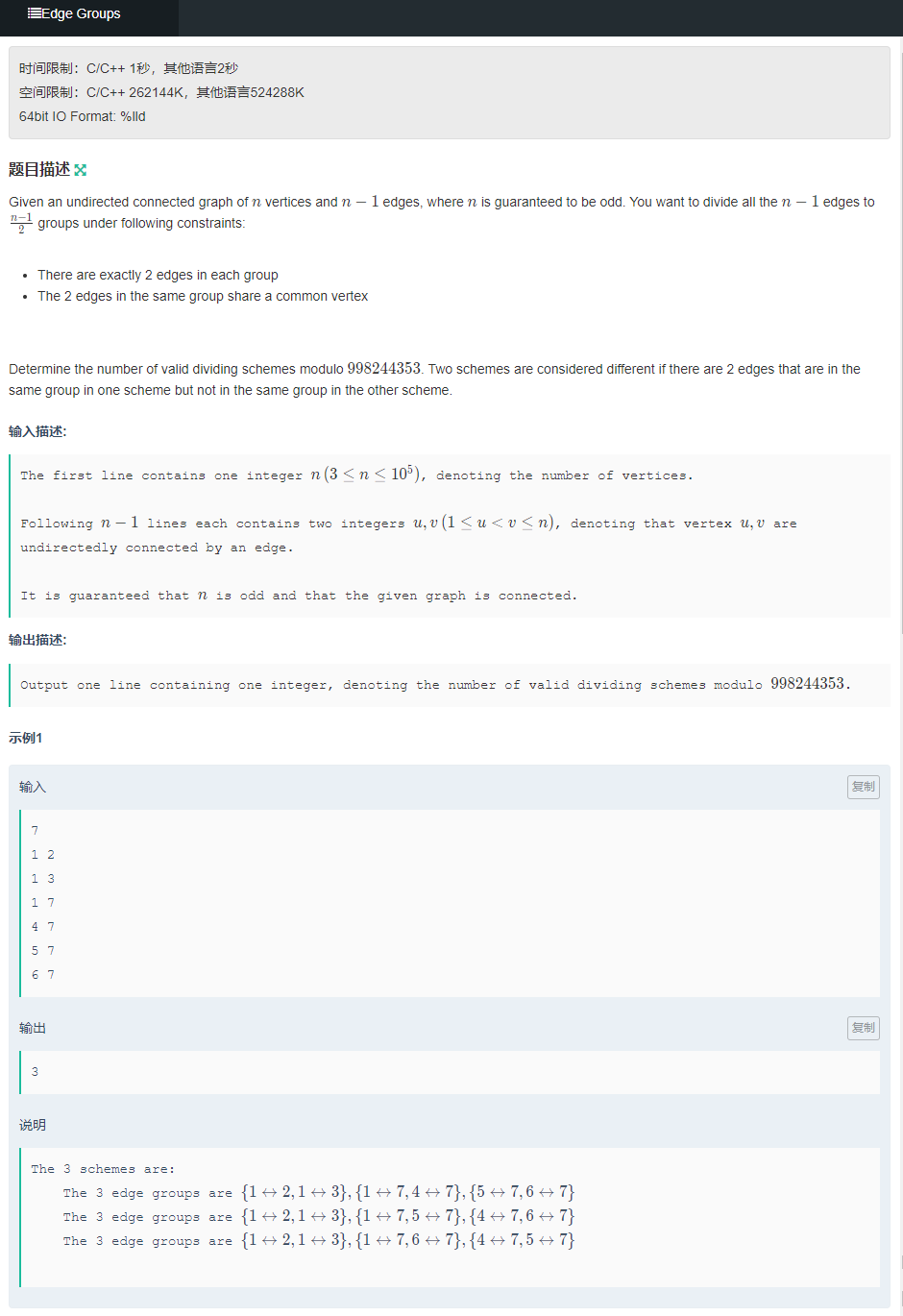
从下往上考虑。并把边转换为点看(感觉会更容易点)具体看代码
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define int long long
6 #define pb push_back
7
8 const int N = 2e5+100 ,inf = 0x3f3f3f3f ,mod = 998244353;
9
10 //*******************Slove
11 int n;
12 vector<int> g[N];
13 int p[N];
14 int sz[N];
15 int slove(int num){
16 int s=1;
17 for(int i=num-1;i>=1;i-=2){
18 s%=mod,s=s*i,s%=mod;
19 }
20 return s;
21 }
22 int ans=1;
23 int dfs(int u,int fa){
24 int sum=0;
25 for(int i=0;i<g[u].size();i++){
26 int to=g[u][i];
27 if(to==fa) continue;
28 sum+=dfs(to,u);
29
30 }
31 if(sum%2){
32 ans=(ans*(slove(sum-1)*sum%mod))%mod;
33
34 return 0;
35 }else{
36 ans=(ans*slove(sum))%mod;
37 return 1;
38 }
39 }
40 signed main(){
41 ans=1;
42 cin>>n;
43 int aa,bb;
44 for(int i=1;i<n;i++){
45 scanf("%lld%lld",&aa,&bb);
46 g[aa].pb(bb),g[bb].pb(aa);
47 }
48 dfs(1,0);
49 cout<<ans<<endl;
50 return 0;
51 }
52 /* */
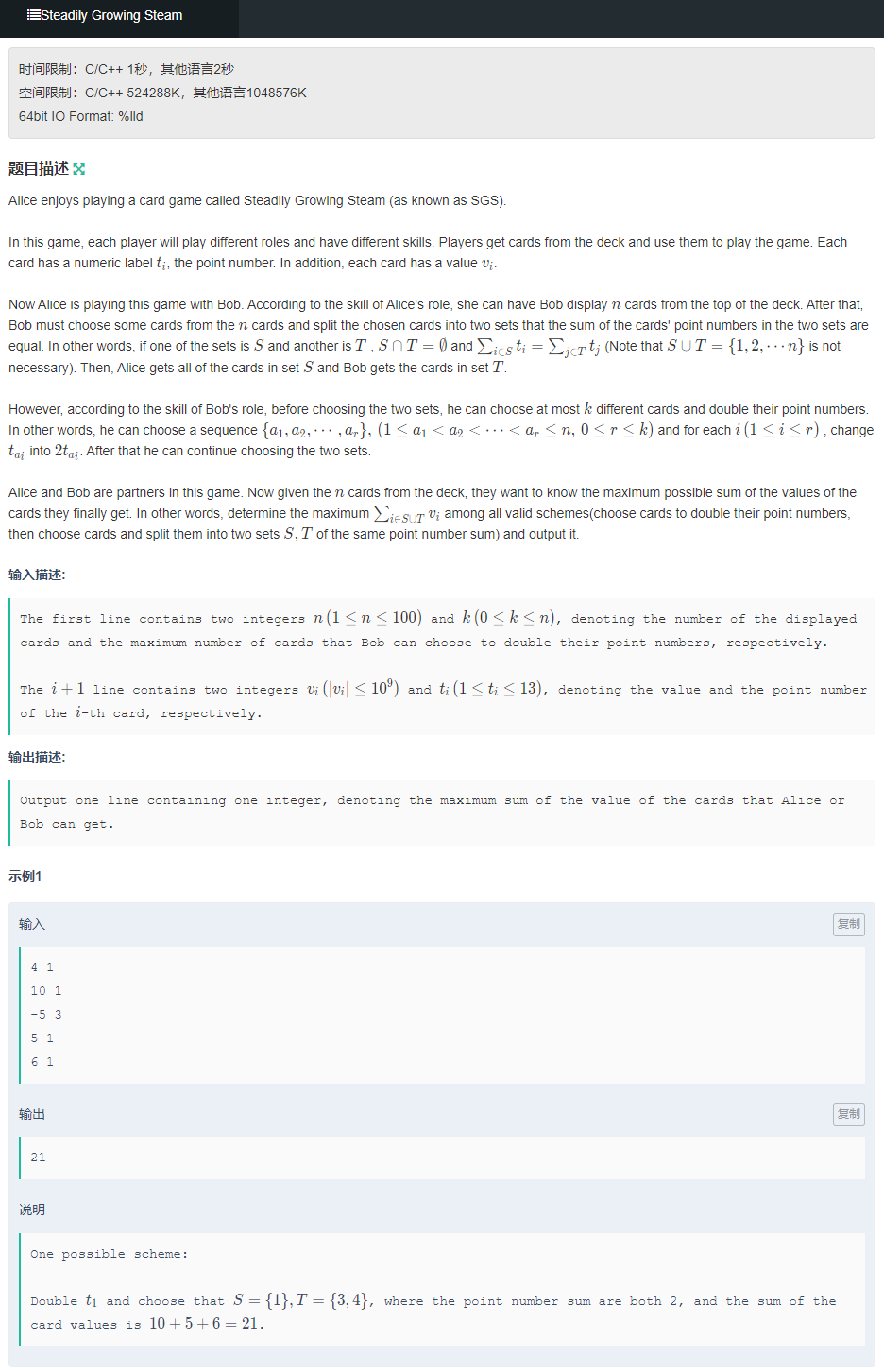
这题可以用用动态规划解决,因为当前状态跟上一个状态有关。假设DP(a,b,c)表示当前已经处理到第a位,用了b个功能(功能:*2的功能),且SET(S)-SET(T)的差值为c 。
转移方程大致为:
dp[a][b][c]=max(dp[a-1][b][c-t[i]]+v[i],dp[a][b][c]);
dp[a][b][c]=max(dp[a-1][b][c+t[i]]+v[i],dp[a][b][c]);
dp[a][b][c]=max(dp[a-1][b-1][c-2*t[i]],dp[a][b][c]);
dp[a][b][c]=max(dp[a-1][b-1][c+2*t[i]],dp[a][b][c]);
最后的ANS:max(ans,dp[~][k][~])
注意转移的写法!
1 //dp[a][b][c]:表示已经处理到第a位,当前用了dou b个元素,且差值为c。
2 #include<bits/stdc++.h>
3 using namespace std;
4 #define int long long
5 const int N = 109 , inf = 1e14 , M = 2700;//M:表示当前的原点位置,基准位置
6 int n,k;
7 int v[N],t[N];
8 int dp[N][N][M*2+100];
9 signed main(){
10 cin>>n>>k;
11 for(int i=1;i<=n;i++) scanf("%lld%lld",&v[i],&t[i]);
12 for(int a=0;a<=n;a++){
13 for(int b=0;b<=101;b++){
14 for(int c=0;c<=2*M;c++)
15 dp[a][b][c]=-inf;
16 }
17 }
18 dp[0][0][M]=0;
19
20 for(int a=1;a<=n;a++){
21 for(int b=0;b<=min(a,k);b++){
22 for(int c=0;c<=2*M;c++){
23 dp[a][b][c]=max(dp[a-1][b][c],dp[a][b][c]);
24 if(c-t[a]>=0) dp[a][b][c]=max(dp[a-1][b][c-t[a]]+v[a],dp[a][b][c]);
25 if(c+t[a]<=2*M) dp[a][b][c]=max(dp[a-1][b][c+t[a]]+v[a],dp[a][b][c]);
26 if(b-1>=0&&c-2*t[a]>=0) dp[a][b][c]=max(dp[a-1][b-1][c-2*t[a]]+v[a],dp[a][b][c]);
27 if(b-1>=0&&c+2*t[a]<=2*M) dp[a][b][c]=max(dp[a-1][b-1][c+2*t[a]]+v[a],dp[a][b][c]);
28 }
29 }
30 }
31 int ans=0;
32 for(int i=1;i<=n;i++){
33 for(int j=0;j<=min(i,k);j++)
34 ans=max(ans,dp[i][j][M]);
35 }
36 cout<<ans;
37 return 0;
38 }
39 /*
40 dp[a][b][c]=max(dp[a-1][b][c-t[i]]+v[i],dp[a][b][c]);
41 dp[a][b][c]=max(dp[a-1][b][c+t[i]]+v[i],dp[a][b][c]);
42 dp[a][b][c]=max(dp[a-1][b-1][c-2*t[i]],dp[a][b][c]);
43 dp[a][b][c]=max(dp[a-1][b-1][c+2*t[i]],dp[a][b][c]);
44
45 ans=max(ans,dp[n][k][~]);
46 */



