Educational Codeforces Round 80 (Rated for Div. 2)【A,B,C,D】C题DP{GG了} D题【数组转化成二进制形式判断+二分】

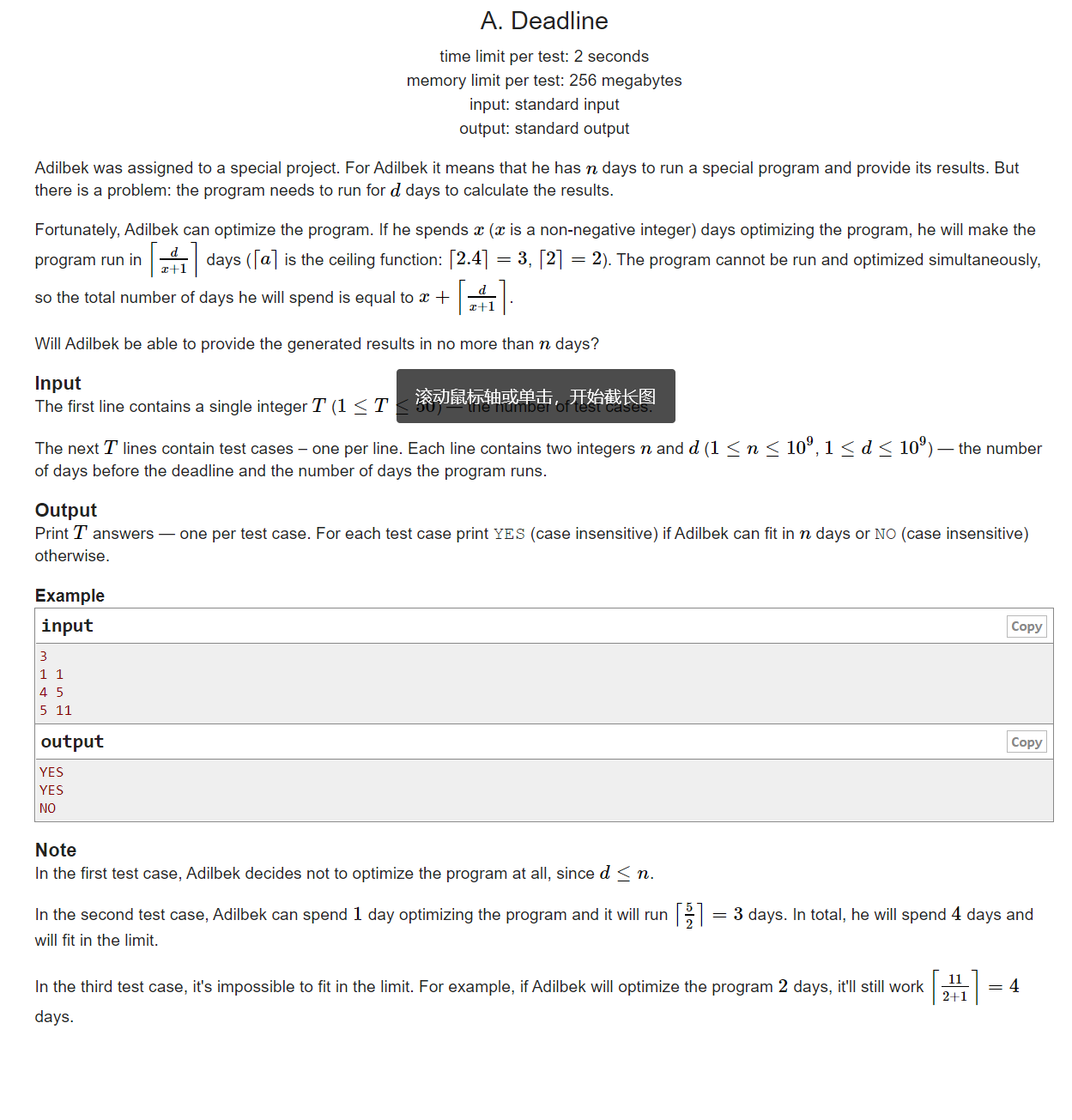
 A题直接暴力水过

#include<bits/stdc++.h>
 
using namespace std;
#define int long long 
#define N 6666666
int arr[N];
 
signed main(){
    int _;cin>>_;
    while(_--){
        int n,m;
        cin>>n>>m;
        if(n>=m){
            cout<<"YES"<<'
';
            continue;
        }
        int f=0;
        for(int i=1;i<n;i++){
            int t=m/(i+1);
            if(m%(i+1)) t++;
            if(i+t<=n){
                f=1;
                break;
            }
        }
        if(f){
            cout<<"YES"<<'
';
        }else{
            cout<<"NO"<<'
';
        }
    }
    return 0;
}

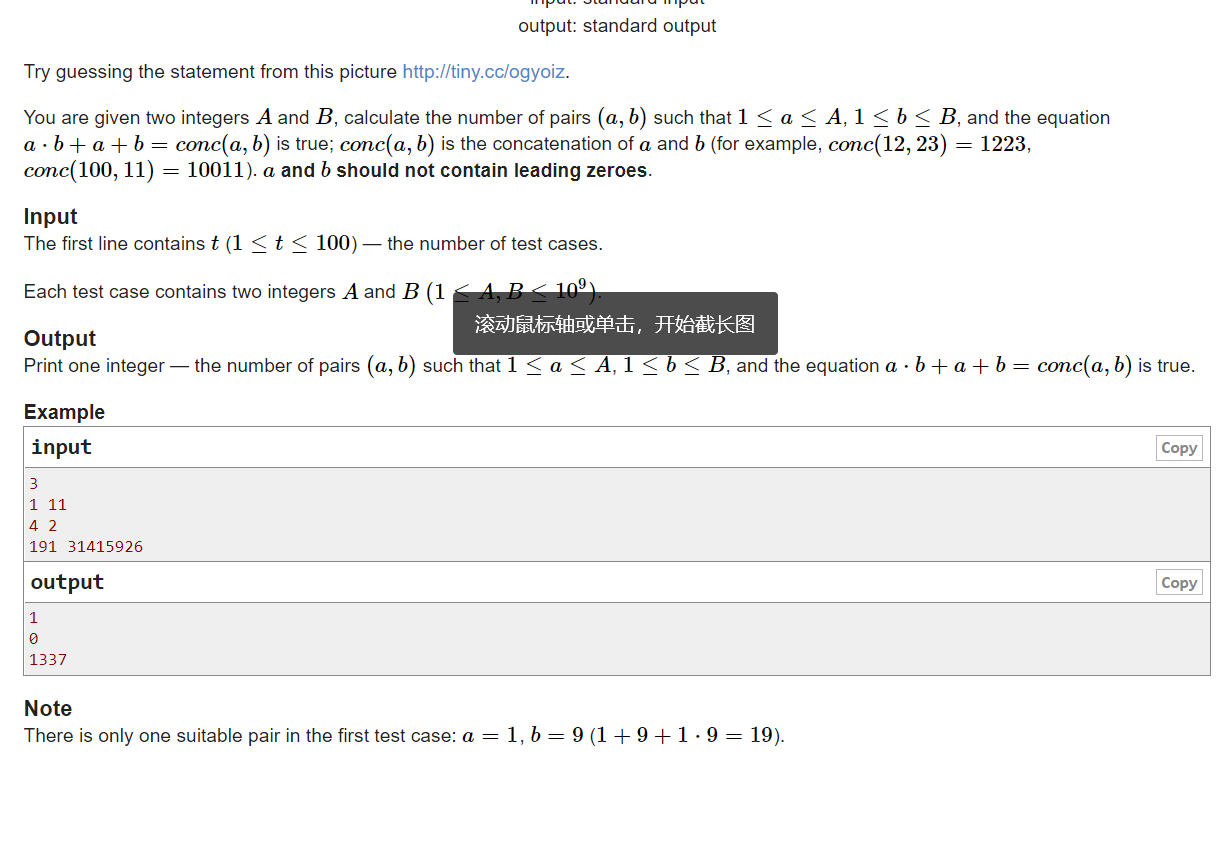
 暴力打了个表看出的规律。

#include<bits/stdc++.h>
 
using namespace std;
#define int long long 
#define N 6666666
int arr[N];
 
signed main(){
    int _;cin>>_;
    while(_--){
        int a,b;
        cin>>a>>b;
        if(b<9){
            cout<<"0"<<'
';
            continue;
        }
        int s=0;int cnt=0;
        for(int i=0;;i++){
            s=s*10+9;
            
            if(s>b){
                
                break;
            }cnt++;
            
        }
        cout<<cnt*a<<'
';
    }
    return 0;
}

 不会DPQAQ

• 题意：用n个数字(1~n)，构造两个长度为m的序列满足以下条件：

  • ai≤bi(1≤i≤m)​
    
  • a序列不递减
  • b序列不递增

  问有多少种方案？

• 分析：

• 根据a不递减，b不递增，且ai≤bi(1≤i≤m)ai≤bi(1≤i≤m) 的条件，我们可以得出如果将b序列反向加在a序列后面构成新的序列，这个序列一定是非递减的。所以问题转为2*m的序列，用n个数构成非递减序列的方案数。DP。
• dp[i][j]表示第 i 个位置放 j 数的方案数，显然它等于前面 i - 1 位放 k (k≤j) 的方案数之和

• #include<bits/stdc++.h>
   
  using namespace std;
  #define int long long
  #define mod 1000000007
  int dp[2000][2000];//
  //dp[i][j]表示第 i 个位置放 j 数的方案数，
  //显然它等于前面 i - 1 位放 k (k≤j) 的方案数之和。
  signed main(){
      int n,m;
      int ans=0;
      cin>>n>>m;
      for(int i=1;i<=n;i++) dp[1][i]=1;
      for(int i=2;i<=2*m;i++){
          for(int j=1;j<=n;j++){
              for(int k=1;k<=j;k++){
                  dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;
              }
          }
      }
      for(int i=1;i<=n;i++){
          ans=ans+dp[2*m][i];
          ans=ans%mod;
      }
      cout<<ans;
      return 0;
  } 

  

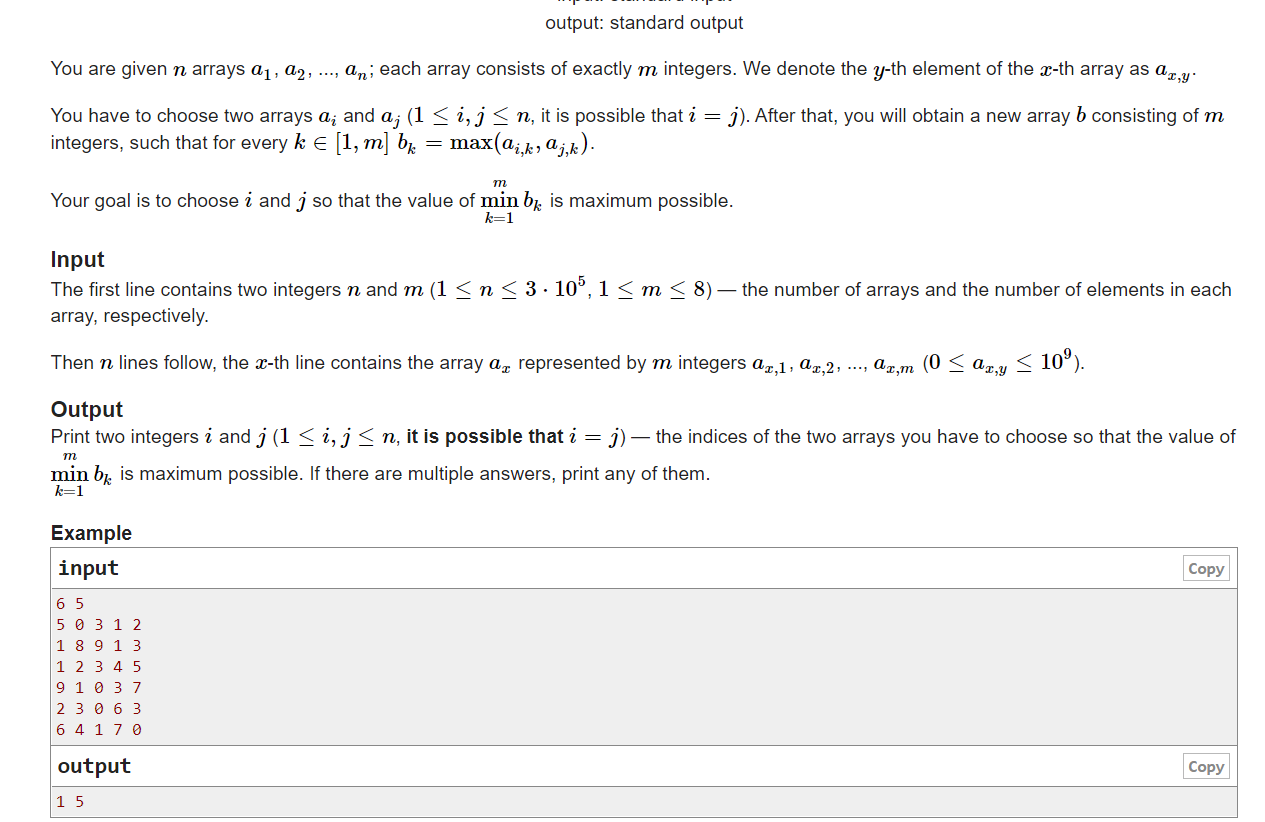
  二分 

• 二分的check如何判断

  check(x)思路，把数组转化成二进制形式，如果当前为大于x,则改位二进制数为1，否则为零，最后的到的二进制数即可替代数组。

• #include<bits/stdc++.h>
  using namespace std;
  #define int long long
  #define N 300009
  int arr[N][20];
  int vis[N];
  int n,m;
  int ansx,ansy;
  int check(int K){
      for(int i=0;i<=300;i++) vis[i]=0;
      for(int i=1;i<=n;i++){
          int sum=0;
          for(int j=1;j<=m;j++){
              if(arr[i][j]>=K)
                  sum|=1<<(j-1);
          }
          vis[sum]=i;
      }
      for(int i=0;i<=256;i++){
          for(int j=0;j<=256;j++){
              if(vis[i]&&vis[j]&&(((1<<m)-1)==(i|j))){
                  ansx=vis[i];
                  ansy=vis[j];
                  return 1;
              }
          }
      }
      return 0;
  }
  signed main(){
      cin>>n>>m;
      for(int i=1;i<=n;i++)
          for(int j=1;j<=m;j++)
              cin>>arr[i][j];
      int l=0;int r=1000000000;
      ansx=0;
      ansy=0;
      while(l<=r){
          int mid=(l+r)/2;
          if(check(mid)){
              l=mid+1;
          }else{
              r=mid-1;
          }
      }
      cout<<ansx<<" "<<ansy;
      return 0;
  }