题目背景
众周所知,在西洋棋中,我们有城堡、骑士、皇后、主教和长脖子鹿。
题目描述
如图所示,西洋棋的“长脖子鹿”,类似于中国象棋的马,但按照“目”字攻击,且没有中国象棋“别马腿”的规则。(因为长脖子鹿没有马腿)
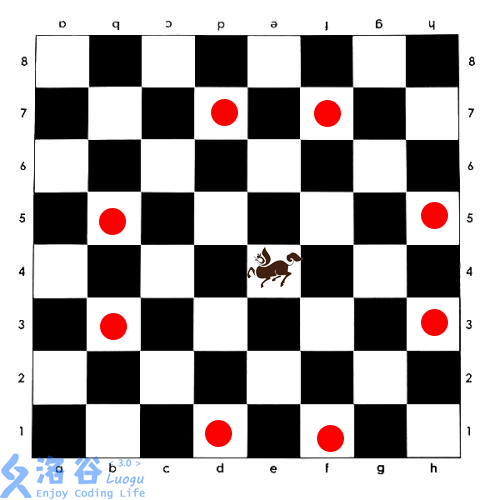
给定一个N * MN∗M,的棋盘,有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。
输入格式
输入的第一行为两个正整数NN,MM,KK。其中KK表示禁止放置长脖子鹿的格子数。
第22~第K+1K+1行每一行为两个整数Xi, YiXi,Yi,表示禁止放置的格子。
输出格式
一行一个正整数,表示最多能放置的长脖子鹿个数。
输入输出样例
输入 #1
2 2 1 1 1
输出 #1
3
输入 #2
/*额外提供一组数据*/ 8 7 5 1 1 5 4 2 3 4 7 8 3
输出 #2
28
思路:
-
首先我们看,在棋盘上放棋子,让他们互相不能攻击,这明显是到二分图最大独立集(类似题骑士共存问题)
-
接着我们想怎样染色,第一下想的就是像棋盘那样按行列奇偶性来染,但是显然不对。于是我们发现一个惊人的问题,基数行和偶数行之间的棋子不会互相攻击!!!这样就好了,按行奇偶性来染色,跑个二分图最大独立集就行(二分图最大独立集=点数-最大匹配数)
80分的代码QAQ:
1 #include<bits/stdc++.h> 2 3 //最大独立集=n-最小点覆盖 4 using namespace std; 5 #define maxn 6666 6 int dx[]={1,1,3,3,-1,-1,-3,-3}; 7 int dy[]={3,-3,1,-1,3,-3,1,-1}; 8 int mp[maxn][maxn]; 9 int match[666*666]; 10 int vis[40001]; 11 int num[maxn][maxn]; 12 int flag=0; 13 int n,m,k; 14 int head[maxn*maxn]; 15 inline int read(){ 16 char c = getchar(); int x = 0, f = 1; 17 while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} 18 while(c >= '0' & c <= '9') x = x * 10 + c - '0', c = getchar(); 19 return x * f; 20 } 21 struct Edge{ 22 int to,next; 23 }e[666*666*4]; 24 void add(int u,int v){ 25 flag++; 26 e[flag].to=v; 27 e[flag].next=head[u]; 28 head[u]=flag; 29 } 30 inline int cal_note(int xx,int yy){ //计算该格子的编号 31 return (xx-1)*n+yy; 32 } 33 int dfs(int u){ 34 for(register int i=head[u];i;i=e[i].next){ 35 int temp=e[i].to; 36 if(!vis[temp]){ 37 vis[temp]=1; 38 if(match[temp]==0||dfs(match[temp])) 39 { 40 match[temp]=u; 41 return 1; 42 } 43 } 44 } 45 return 0; 46 } 47 int main(){ 48 //int n,m; 49 //scanf("%d%d",&n,&m); 50 n=read(); 51 m=read(); 52 k=read(); 53 int xx,yy; 54 for(int i=1;i<=k;i++){ 55 //scanf("%d%d",&x,&y); 56 xx=read(); 57 yy=read(); 58 mp[xx][yy]=1;// 标记不可以走到的点 59 } 60 int cnt=0; 61 /*for(int i=1;i<=n;i++) 62 for(int j=1;j<=m;j++) 63 num[i][j]=++cnt; // 给每一个点编号 */ 64 for(register int i=1;i<=n;i+=2){ 65 for(register int j=1;j<=m;j++){ 66 if(mp[i][j]) 67 continue; 68 else{ 69 int x=i; 70 int y=j; 71 for(int k=0;k<8;k++){ 72 int tx=x+dx[k]; 73 int ty=y+dy[k]; 74 if(tx>=1&&ty>=1&&tx<=n&&ty<=m&&!mp[tx][ty]){ 75 //v[num[x][y]].push_back(num[tx][ty]); 76 //v[num[tx][ty]].push_back(num[x][y]); 77 add(cal_note(i,j),cal_note(tx,ty)); 78 // add(cal_note(tx,ty),cal_note(x,y)); 79 } 80 } 81 } 82 } 83 } 84 int ans=0; 85 for(register int i=1;i<=n;i+=2){ 86 for(register int j=1;j<=m;j++){ 87 if(mp[i][j]) 88 continue; 89 memset(vis,0,sizeof(vis)); 90 if(dfs(cal_note(i,j))) 91 ans++; 92 } 93 } 94 int res=n*m-k-ans; 95 printf("%d ",res); 96 return 0; 97 }