数字信号处理 － Chap7 DFT和FFT （1）DFT基础

7.1 DFT基础

DTFT（离散时间傅里叶变换） 的采样点无限，难以利用计算机实现。DFT（离散傅里叶变换）解决了这一问题，仅需有限采样点，其定义为：

                          

1）DFT同样给出了信号的频率分量，k标记每个分量的频率

2）DFT输入的时域采样x[n]的个数＝输出的频率采样X[k]的个数，都为N。可把这N个时域采样点看成是位于DFT窗中，窗的长度等于采样点数N，位于窗外的采样点不影响分析。

3）相对于DTFT 定义在无限个频率上，DFT的X[k]定义在有限个标号k上，易于处理

4）DFT的周期为N

X[k]的复数形式为

                       

1）幅度频谱： 对k的图形

2）相位频谱： 对k的图形

7.1.1 DFT与DTFT的关系

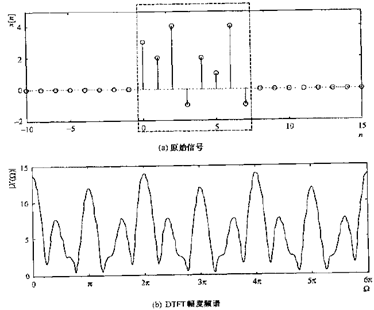
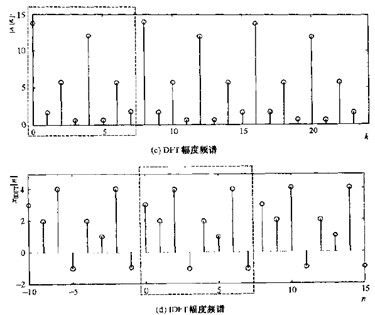
对同一个时域有限点的采样信号，其DFT和DTFT一样。DTFT得到的频谱是光滑的，而DFT则是这一光谱频谱的采样形式，如下图

                 

1）图b是DTFT幅度频谱。注：非周期信号的2pi周期性

2）图c是DFT幅度频谱，它是DTFT的采样形式

3）图d是逆DFT，它不是原始非周期信号，而是其周期形式

7.1.2 DFT的频率分辨率

利用欧拉公式，DFT可写为

                    

1）信号 与正弦越相关，频谱分量X[k]就越大

2）DFT可看作是窄带滤波器组：每个频谱分量X[k]可看作是窄带滤波器的输出，此窄带滤波器的中心位于数字频率 弧度。

 

DFT的N个点覆盖了0到fs（采样频率）的范围，因此其频率采样间隔为fs/N，它就是DFT的频率分辨率（描述了DFT区分相邻信号频率的能力）。

1）采样频率fs不变，则采样点N越多，分辨率越好

2）从滤波器组的角度看，分辨率好的DFT是由大量非常窄的带通滤波组成

7.1.3 DFT的“墨斑”特性

尽管计算DFT仅需要N各点，但其中也有重复信息。由于DFT点位于kfs/N，因此当k=N/2达到fs/2的奈奎斯特界限时

1）这时k=0到N/2的DFT点携带了DFT全部必要的幅度和相位信息

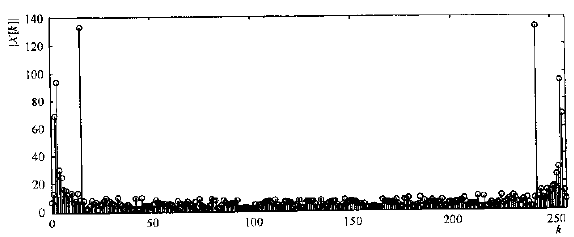
2）其余点仅是基带重要信号频率的镜像副本（采样的人为结果）。对幅度频谱来说，其这点与k=0到N/2的点关于N/2对称，称为“墨斑”特性。如下图DFT幅度频谱关于N/2＝128对称，频谱后半部分的峰是基带频率的镜像。

7.1.4 真实频率的模糊 

DFT不能超越分辨率所允许的范围去准确定位频率。如以fs=6.4Hz对包含1/16和3/8频率的信号进行采样，然后用256DFT分析。此时分辨率为6.4/256＝0.025Hz，因为DFT分量仅在0.025Hz整数倍处，而(1/16)/0.025=2.5，因此1/16Hz的信号不能准确定位，只能用其两侧任一侧的DFT标号去描述；而(3/8)/0.025=15，可被准确定位。

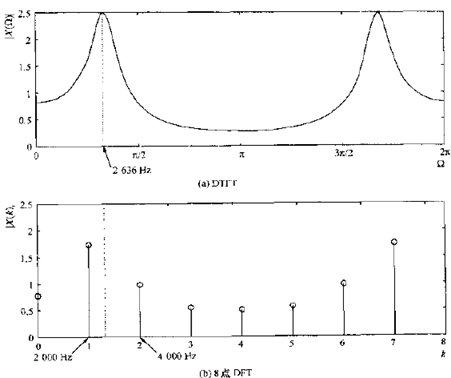
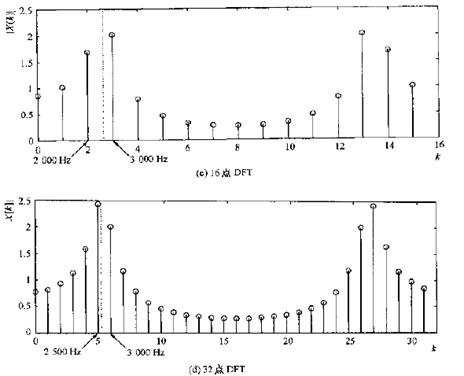
当DFT没有频率与所分析信号的重要频率相符时，就导致真实频率的模糊。如下图所示

  

1）图a：以16Hz采样信号的DTFT。在数字频率 处有一谱峰，对应模拟频率 2636Hz

1）图b~d：DFT所用点数越多，就越接近求出真实的2636Hz的频率。最大DFT峰总在最接近这个频率的DFT标号处。但所有结果都造成一定程度的峰值模糊。