参考文章:【http://blog.163.com/gc_chdch@126/blog/static/172279052201639103637601/】
树的欧拉序是对树进行DFS的一种序列。有两种形式:1、在每个结点进和出都加进序列。2、只要到达每一个结点就把他加进序列。
例如:给出一棵树:
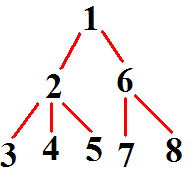
第一种方法得到的序列和对应的进出状态分别是:
1 2 3 3 4 4 5 5 2 6 7 7 8 8 6 1
进 进 进 出 进 出 进 出 出 进 进 出 进 出 出 出
(每个结点恰好出现了两次)
用这个序列可以解决树上求和的问题:
1、求某个点到根节点的额权值和。方法是:需要在进的点处做加法,出的点处做减法,查询某点就只需要查询对应的前缀即可。
*2、求某个子树的权值和。方法是:需要在进的点处做加法,求某个点最后一次出现的位置的前缀和减去第一次出现的位置的前一个位置的前缀和即可。
第二种方法得到的序列是:
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1
用这一个序列,可以解决的一个问题是:
1、求某两点的LCA。显然这两点之间的区间中,深度最小点就是LCA。这可以用RMQ解决。
2、求某个子树的权值和,方法是:只记录第一次出现的数的值,同样的查询某点就只需要查询该点在欧拉序中最后出现的位置的前缀即可减去第一次出现的额位置-1的前缀和即可。
3、换根操作:这种欧拉序相当于以根为起点围着树跑了一圈,那么我们就可以把欧拉序写成一个环就是:
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
以某个点为跟的欧拉序就是以某个点在上面的欧拉序中第一次出现的位置为起点向前走(2*n-1)步,例如以4为根的欧拉序就是
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
L-------------------------------------------------R//以4为跟的欧拉序,同时可以维护和之类的东西。