Link.
P.S.
和 @Lillia 从 8:00 嘴巴到 8:45,总算嘴巴出来了个做法。
Solution.
首先,画一张 时间-位置 图。

如果有这样的商店,容易证明它搭乘向左的列车肯定不劣,我们定义它为左箭头。
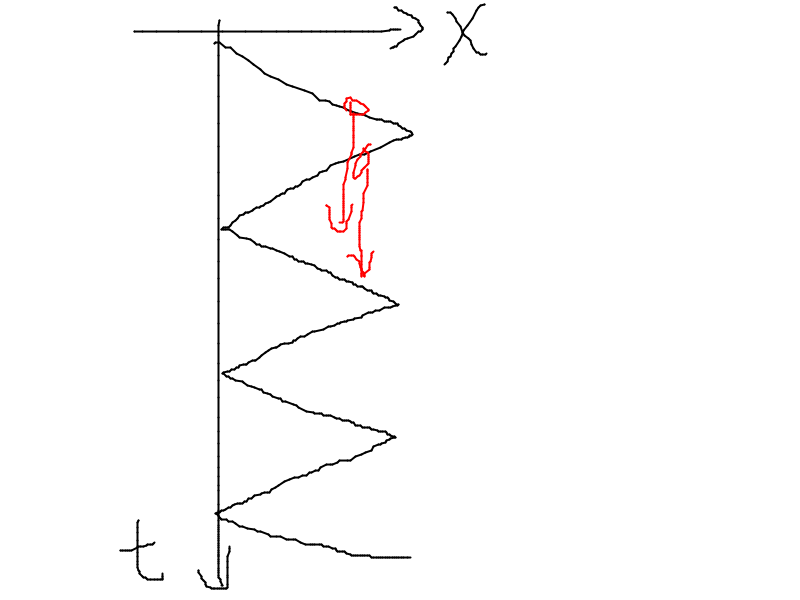
同理,左边也会有只能向右的箭头,定义为右箭头。
当然还有不左不右的箭头,又需要分类。
有种商店,定义为同向商店,下车和上车列车前进方向相同。
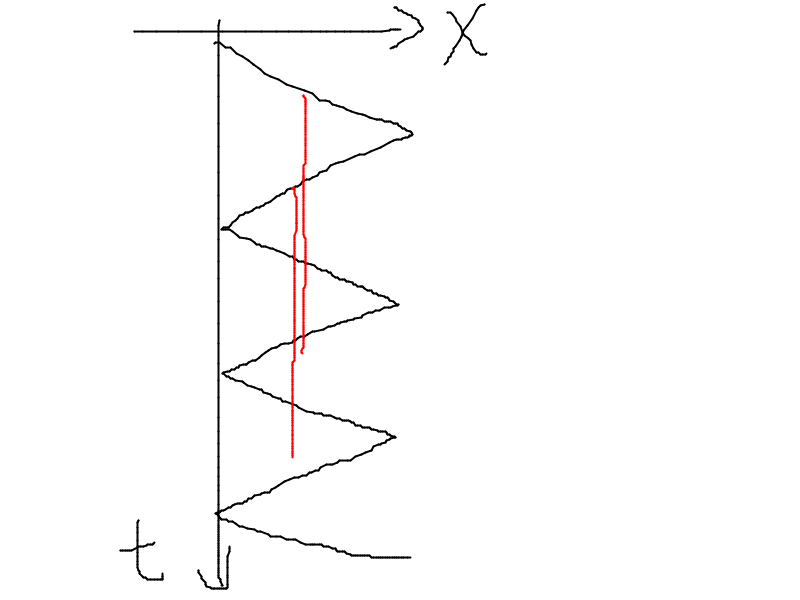
当然还有不同向商店(如图
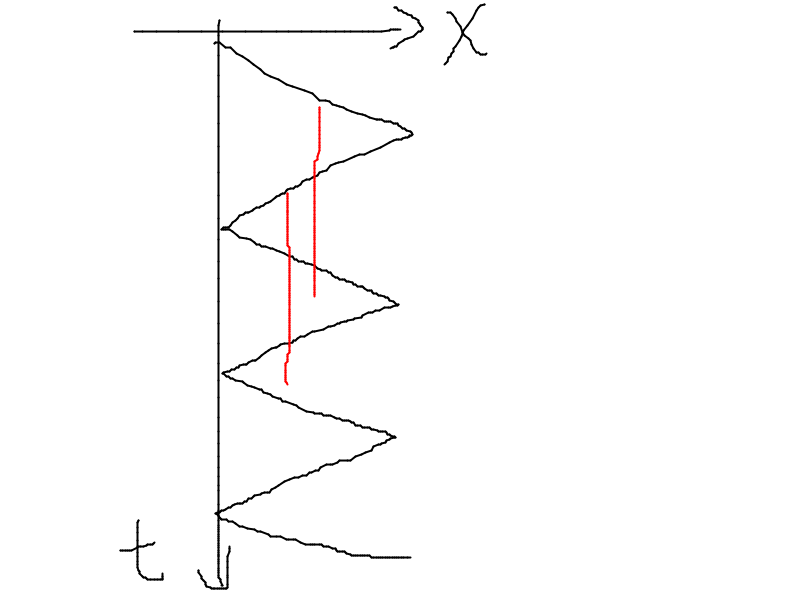
有一些比较显然的性质:
- 不存在一个左箭头它在右箭头左边
- 证明的话直接考虑左箭头必须在序列的中点左边,右箭头必须在序列中点右边即可
- 同向商店完全没有用,直接在列车经过它时消费掉即可
- 证明就考虑根本没法优化,前后本质相同。
然后把同向商店去掉后,不同向商店本质上来说就是一个既可以当作左箭头又可以当作右箭头的箭头,称它为双向箭头。
原问题转化成了有很多箭头,需要把它划分成尽量少个存在合法排序方式的子集。
一个序列合法当且仅当如果存在,每个箭头的后继相对于当前这个箭头的方向就是这个箭头指向的方向。
不就是在每个箭头上往那边前进找到下一个嘛。。。
考虑它其实是有后效性的。
就是因为配对了一对商店后下一个来回的开头就不能使用了。
但是可以通过贪心把后效性优化掉。
考虑从左往右扫,每次遇到一个右括号贪心匹配,这样每个开头都不会被影响到。
所以可以直接不考虑顺序匹配。
那就变成了括号匹配问题,贪心匹配即可。
根据之前的性质,不难发现贪心让左边和右边留下尽量多的再匹配即可。
Coding.
点击查看代码
//是啊,你就是那只鬼了,所以被你碰到以后,就轮到我变成鬼了{{{
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
template<typename T>inline void read(T &x)
{
x=0;char c=getchar(),f=0;
for(;c<48||c>57;c=getchar()) if(!(c^45)) f=1;
for(;c>=48&&c<=57;c=getchar()) x=(x<<1)+(x<<3)+(c^48);
f?x=-x:x;
}
template<typename T,typename...L>inline void read(T &x,L&...l) {read(x),read(l...);}/*}}}*/
int n,L,a[300005],t[300005],rs=0;char r[300005],l[300005];
int main()
{
read(n,L);for(int i=1;i<=n;i++) read(a[i]);
rs=1+n,L<<=1;for(int i=1;i<=n;i++) read(t[i]),rs+=(t[i]-1)/L,t[i]=(t[i]-1)%L+1;
for(int i=1;i<=n;i++) l[i]=(a[i]*2>=t[i]),r[i]=(L-a[i]*2>=t[i]);
rs-=r[n];int pt=0,tp=0,wh=n;
for(int i=1;i<n;i++) if(!l[i]&&!r[i]) continue;
else if(!r[i]) {wh=i;break;}else if(l[i]) tp++;else if(tp) tp--,rs--;
for(int i=n-1;i>=wh;i--) if(!l[i]&&!r[i]) continue;
else if(!l[i]) break;else if(r[i]) pt++;else if(pt) pt--,rs--;
return printf("%lld\n",1ll*L*(rs-((pt+tp)>>1))),0;
}