Fast Fourier Transform
首先介绍几个概念:
1.卷积:设f(x)和g(x)是两个可积函数,令![]() 那么h(x)就是f(x)和g(x)的卷积
那么h(x)就是f(x)和g(x)的卷积
但更常用的是离散的情况:![]()
卷积的意义:如下图
首先将两个函数都用T来表示。
对其中一个函数做水平翻转:g(T)→g(-T).
加上一个时间偏移量,让g(t-T)能沿着 au轴滑动。
让t从-∞滑动到+∞。两函数交会时,计算交会范围中两函数乘积的积分值。
换句话说,我们是在计算一个滑动的的加权平均值。也就是使用g(-T).当做加权函数,来对f(T)取加权平均值。
最后得到的波形(未包含在此图中)就是f和g的卷积。

2.时域和频域:如下图
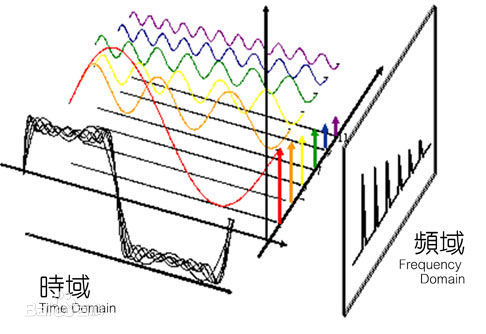
时域:可以理解为随时间变化
频域:把f(x)拆成若干个正弦波之后每个正弦波的强度。和每个正弦波的频率有关
如下图,傅里叶变换将函数的时域(红色)与频域(蓝色)相关联。频谱中的不同成分频率在频域中以峰值形式表示。

离散傅里叶变换(DFT)把时域信号变换为频域信号
时域乘积,频域卷积;频域卷积,时域乘积
而其逆变换(IDFT) vice versa
Reference:
Wikipedia