poj2284 欧拉公式

题意：给出一图形，求该图形把平面分成了几部分

欧拉公式：　　http://blog.csdn.net/wangxiaojun911/article/details/4586550

对于二维平面上的情况。设图形上有V个点，E条边，把平面分成了F个独立的部分，那么满足V+F-E=2

如下图：

             

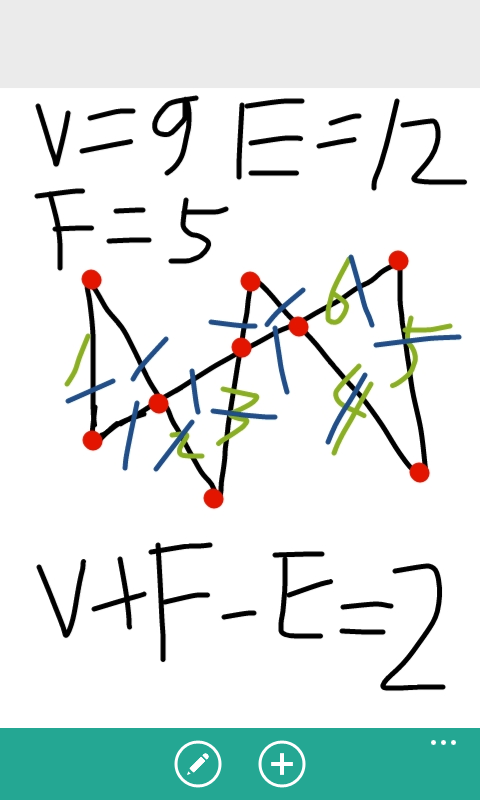
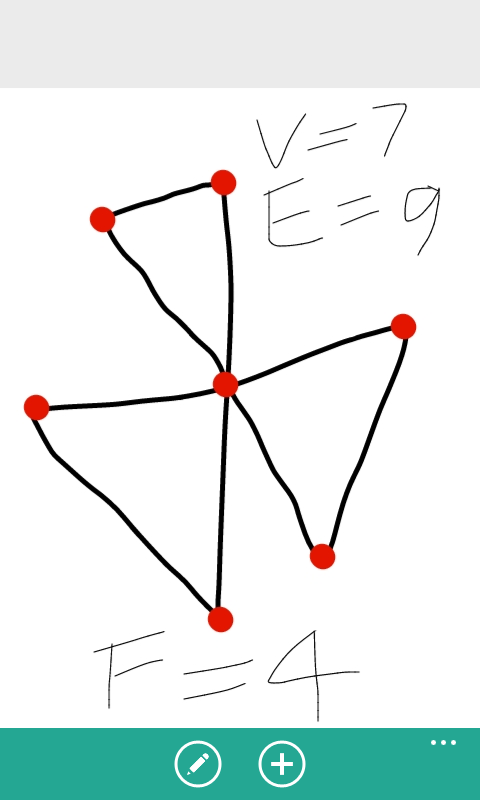
那么求F就转化成了如何求V和E

求V：枚举任意两线段的交点即可。注意可能出现三线共点的情况，要判重。

求E：某线段上的n个点会把这条线段分成n-1部分。用这个性质再YY一下就好了。

注意：

1.这里判重不能用map，因为交点的计算结果肯定是有精度误差的，再hash一下就没法判重了。

　　我用的方法是手艹了一个破vector，实际上有更简洁的方法.....

     先排序，使重复的元素在数组里相邻。再用STL里的unique即可轻松实现去重

     （ Reference：http://blog.sina.com.cn/s/blog_a389f34a01013itn.html）

2.模板里的求两线段交点代码没有考虑这种情况：

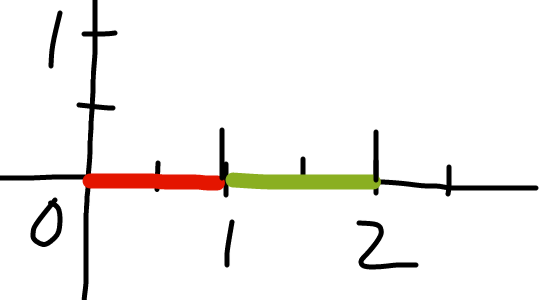
如图，两线段分别为【(0,0)->(0,1)】和【(0,1)->(0,2)】

模板代码认为他们是不香蕉的= =  哼

所以这里要处理一下：

（大白书上lrj模板也存在这个问题）

    //求两线交点
    point crosspoint(line v)
    {
        if ((point_cmp(a,v.a))||(point_cmp(a,v.b)))     return a;
        if ((point_cmp(b,v.a))||(point_cmp(b,v.b)))     return b;        //处理端点处相交的情况
        double a1=v.b.sub(v.a).det(a.sub(v.a));
        double a2=v.b.sub(v.a).det(b.sub(v.a));
        return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
    }

AC  Code：

#include<vector>
#include<list>
#include<map>
#include<set>
#include<deque>
#include<queue>
#include<stack>
#include<bitset>
#include<algorithm>
#include<functional>
#include<numeric>
#include<utility>
#include<iostream>
#include<sstream>
#include<iomanip>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cctype>
#include<string>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<ctime>
#include<climits>
#include<complex>
#define mp make_pair
#define pb push_back
using namespace std;
const double eps=1e-8;//精度
const double pi=acos(-1.0);//π
const double inf=1e20;//无穷大
const int maxp=1111;//最大点数
/*
    判断d是否在精度内等于0
*/
int dblcmp(double d)
{
    if (fabs(d)<eps)return 0;
    return d>eps?1:-1;
}


bool dcmp(double x)
{
    return (fabs(x)<eps);
}

/*
    求x的平方
*/
inline double sqr(double x){return x*x;}
/*
    点/向量
*/
struct point
{
    double x,y;
    point(){}
    point(double _x,double _y):x(_x),y(_y){};
    //读入一个点
    void input()
    {
        scanf("%lf%lf",&x,&y);
    }
    //输出一个点
    void output()
    {
        printf("%.2f %.2f
",x,y);
    }
    //判断两点是否相等
    bool operator==(point a)const
    {
        return dblcmp(a.x-x)==0&&dblcmp(a.y-y)==0;
    }
    //判断两点大小
    bool operator<(point a)const
    {
        return dblcmp(a.x-x)==0?dblcmp(y-a.y)<0:x<a.x;
    }
    //点到源点的距离/向量的长度
    double len()
    {
        return hypot(x,y);
    }
    //点到源点距离的平方
    double len2()
    {
        return x*x+y*y;
    }
    //两点间的距离
    double distance(point p)
    {
        return hypot(x-p.x,y-p.y);
    }
    //向量加
    point add(point p)
    {
        return point(x+p.x,y+p.y);
    }
    //向量减
    point sub(point p)
    {
        return point(x-p.x,y-p.y);
    }
    //向量乘
    point mul(double b)
    {
        return point(x*b,y*b);
    }
    //向量除
    point div(double b)
    {
        return point(x/b,y/b);
    }
    //点乘
    double dot(point p)
    {
        return x*p.x+y*p.y;
    }
    //叉乘
    double det(point p)
    {
        return x*p.y-y*p.x;
    }
    //XXXXXXX
    double rad(point a,point b)
    {
        point p=*this;
        return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p))));
    }
    //截取长度r
    point trunc(double r)
    {
        double l=len();
        if (!dblcmp(l))return *this;
        r/=l;
        return point(x*r,y*r);
    }
    //左转90度
    point rotleft()
    {
        return point(-y,x);
    }
    //右转90度
    point rotright()
    {
        return point(y,-x);
    }
    //绕点p逆时针旋转angle角度
    point rotate(point p,double angle)
    {
        point v=this->sub(p);
        double c=cos(angle),s=sin(angle);
        return point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
    }
};

bool point_cmp(point a,point b)
{
    return ((dcmp(a.x-b.x))&&(dcmp(a.y-b.y)));
}

/*
    线段/直线
*/
struct line
{
    point a,b;
    line(){}
    line(point _a,point _b)
    {
        a=_a;
        b=_b;
    }
    //判断线段相等
    bool operator==(line v)
    {
        return (a==v.a)&&(b==v.b);
    }
    //点p做倾斜角为angle的射线
    line(point p,double angle)
    {
        a=p;
        if (dblcmp(angle-pi/2)==0)
        {
            b=a.add(point(0,1));
        }
        else
        {
            b=a.add(point(1,tan(angle)));
        }
    }
    //直线一般式ax+by+c=0
    line(double _a,double _b,double _c)
    {
        if (dblcmp(_a)==0)
        {
            a=point(0,-_c/_b);
            b=point(1,-_c/_b);
        }
        else if (dblcmp(_b)==0)
        {
            a=point(-_c/_a,0);
            b=point(-_c/_a,1);
        }
        else
        {
            a=point(0,-_c/_b);
            b=point(1,(-_c-_a)/_b);
        }
    }
    //读入一个线段
    void input()
    {
        a.input();
        b.input();
    }
    //校准线段两点
    void adjust()
    {
        if (b<a)swap(a,b);
    }
    //线段长度
    double length()
    {
        return a.distance(b);
    }
    //直线倾斜角 0<=angle<180
    double angle()
    {
        double k=atan2(b.y-a.y,b.x-a.x);
        if (dblcmp(k)<0)k+=pi;
        if (dblcmp(k-pi)==0)k-=pi;
        return k;
    }
    //点和线段关系
    //1 在逆时针
    //2 在顺时针
    //3 平行
    int relation(point p)
    {
        int c=dblcmp(p.sub(a).det(b.sub(a)));
        if (c<0)return 1;
        if (c>0)return 2;
        return 3;
    }
    //点是否在线段上
    bool pointonseg(point p)
    {
        //if ((p==a) || (p==b))  return true;
        return dblcmp(p.sub(a).det(b.sub(a)))==0&&dblcmp(p.sub(a).dot(p.sub(b)))<=0;
    }
    //两线是否平行
    bool parallel(line v)
    {
        return dblcmp(b.sub(a).det(v.b.sub(v.a)))==0;
    }
    //线段和线段关系
    //0 不相交
    //1 非规范相交
    //2 规范相交
    int segcrossseg(line v)
    {
        int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
        int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
        int d3=dblcmp(v.b.sub(v.a).det(a.sub(v.a)));
        int d4=dblcmp(v.b.sub(v.a).det(b.sub(v.a)));
        if ((d1^d2)==-2&&(d3^d4)==-2)return 2;
        return (d1==0&&dblcmp(v.a.sub(a).dot(v.a.sub(b)))<=0||
                d2==0&&dblcmp(v.b.sub(a).dot(v.b.sub(b)))<=0||
                d3==0&&dblcmp(a.sub(v.a).dot(a.sub(v.b)))<=0||
                d4==0&&dblcmp(b.sub(v.a).dot(b.sub(v.b)))<=0);
    }
    //线段和直线v关系
    int linecrossseg(line v)//*this seg v line
    {
        int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
        int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
        if ((d1^d2)==-2)return 2;
        return (d1==0||d2==0);
    }
    //直线和直线关系
    //0 平行
    //1 重合
    //2 相交
    int linecrossline(line v)
    {
        if ((*this).parallel(v))
        {
            return v.relation(a)==3;
        }
        return 2;
    }
    //求两线交点
    point crosspoint(line v)
    {
        if ((point_cmp(a,v.a))||(point_cmp(a,v.b)))     return a;
        if ((point_cmp(b,v.a))||(point_cmp(b,v.b)))     return b;
        double a1=v.b.sub(v.a).det(a.sub(v.a));
        double a2=v.b.sub(v.a).det(b.sub(v.a));
        return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
    }

    //点p到直线的距离
    double dispointtoline(point p)
    {
        return fabs(p.sub(a).det(b.sub(a)))/length();
    }
    //点p到线段的距离
    double dispointtoseg(point p)
    {
        if (dblcmp(p.sub(b).dot(a.sub(b)))<0||dblcmp(p.sub(a).dot(b.sub(a)))<0)
        {
            return min(p.distance(a),p.distance(b));
        }
        return dispointtoline(p);
    }
    //XXXXXXXX
    point lineprog(point p)
    {
        return a.add(b.sub(a).mul(b.sub(a).dot(p.sub(a))/b.sub(a).len2()));
    }
    //点p关于直线的对称点
    point symmetrypoint(point p)
    {
        point q=lineprog(p);
        return point(2*q.x-p.x,2*q.y-p.y);
    }
};


struct point P[1000];
struct line  L[1000];
int n;
int CASE=0;

int main()
{
    //freopen("in.txt","r",stdin);

    while (cin>>n)
    {
        if (n==0)   break;
        {
            CASE++;
            n--;
            for (int i=1;i<=n+1;i++)
            {
                scanf("%lf%lf",&P[i].x,&P[i].y);
                if (i>=2)
                    L[i-1]=line(point(P[i-1].x,P[i-1].y),point(P[i].x,P[i].y));
            }
            //L[1..n]:line      P[1..n]:point   P[1]==P[n+1]

            vector<point> POINT;
            POINT.clear();

            int pcount=0;       //the number of points
            for (int i=1;i<n;i++)
                for (int j=i+1;j<=n;j++)
                {
                    if (L[i].segcrossseg(L[j])!=0)
                    {
                        point tm=L[i].crosspoint(L[j]);
                        //printf("P:   %.3f   %.3f
",tm.x,tm.y);
                        bool Find=false;
                        for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
                        {
                            point tp=*it;
                            if ((dcmp(tp.x-tm.x))&&(dcmp(tp.y-tm.y)))
                                Find=true;
                        }
                        if (!Find)
                        {
                            pcount++;
                            POINT.push_back(tm);
                        }
                    }
                }

            for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
            {
                point tp=*it;
                //printf("%.5f %.5f
",tp.x,tp.y);
            }

            int lcount=0;
            for (int i=1;i<=n;i++)
            {
                line tm=L[i];
                int tmp=0;
                for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
                {
                    point tp=*it;
                    if (tm.pointonseg(tp))
                        tmp++;
                }
                lcount=lcount+(tmp-1);
            }

            //cout<<pcount<<"   "<<lcount<<endl;
            //cout<<2+lcount-pcount<<endl;
            //Case 1: There are 2 pieces.
            int ans=2+lcount-pcount;
            //if (ans<0)  ans=2;
            printf("Case %d: There are %d pieces.
",CASE,ans);
        }
    }


    return 0;
}

PS：在poj discussion里面有人给出了这样一组数据:

4

0 0 0 1 0 2 0 0　　　　

答案为2

这组数据我过不去 ╮(╯▽╰)╭

不过这种情况本身就够坑的，所以也不影响AC啦 ╮(╯▽╰)╭