返回一个二维整数数组中最大子数组的和

 要求：

1，输入一个二维整形数组，数组里有正数也有负数。

2，二维数组中连续的一个子矩阵组成一个子数组，每个子数组都有一个和,

3，求所有子数组的和的最大值。

设计思路：

参照一维整数数组求解最大子数组的方法，我们想着将二维数组通过行不同，列相加的方法转化为一维整数数组再求解最大子数组之和。

具体实现：先求出每一行的最大子数组之和，之后比较得出最大和MaxSum,然后通过上述方法求二行的最大子数组之和并与MaxSum比较，用MaxSum存放较大值。以此类推，求三行，四行。。。

最后实现最大子数组的输出及其和的输出。

合作过程：

两人合作探讨设计思路；

一人负责分析程序，编写代码；

另一人负责代码复审和代码测试。

主要代码：

  //二维整数数组最大子数组之和
  #include <iostream>
  #include <stdlib.h>
  #include <time.h>
  using namespace std;

  int main()
  {
     int M,N;
     cout << "输入二维数组的行数和列数：" << endl;
     cin >> M >> N;
     int data[M][N],line[N],sum = 0,d1 = 0;
     int MaxSum ,Maxd1,end1[M][N] = {0},end2[M][N] = {0};
     int i_max = 0,j_max = 0;
     srand((unsigned int)time(0));  //保证生成不同的随机数
     cout << "二维数组为：" << endl;
     for (int j = 0;j < M;j++)   //给二维数组的元素赋值并输出，取值范围是-25到25
     {
         for (int k = 0;k < N;k++)
         {
             data[j][k] = rand()%50 - 25;
             cout << data[j][k] << '	';
         }
         cout << endl;
     }
     cout << endl;

     MaxSum = data[0][0];    //初值赋值为数组第一行第一个元素
     Maxd1 = data[0][0];
     for (int i = 0;i < M;i++)
     {
         for (int i1 = 0;i1 < M-i;i1++)//当1行是循环M次
         {
             for (int j = 0;j < N;j++)//赋初值
             {
                 line[j] = 0;
             }
             for (int i2 = i1;i2 <= i1+i;i2++)//每次循环i次赋值
             {
                 for (int j = 0;j < N;j++)
                 {
                     line[j] += data[i2][j];
                 }
             }
             sum = 0;
             for (int k = 0;k < N;k++)
             {
                 sum += line[k];
                 if (sum > MaxSum)
                 {
                     MaxSum = sum;
                     end1[i][i1] = k;
                     i_max = i;       //最大的时候是i行；
                     j_max = i1;
                 }
                 if(sum < 0)
                 {
                     sum = 0;
                 }
             }

             for (int k = N-1;k >= 0;k--)
             {
                 d1 += line[k];
                 if (d1 > Maxd1)
                 {
                     Maxd1 = d1;
                     end2[i][i1] = k;
                 }
                 if(d1 < 0)
                 {
                     d1 = 0;
                 }
             }

         }
     }
     cout << "最大子数组为：" << endl;
     for (int k = 0;k <= i_max;k++)//输出最大子数组元素
     {
         for (int k1 = end2[i_max][j_max];k1 <= end1[i_max][j_max];k1++)
         {
                 cout << data[j_max+k][k1] << '	';
         }
         cout << endl;
     }

     cout << endl;
     cout << "最大子数组的和为： " << MaxSum << endl;
  }

运行截图：

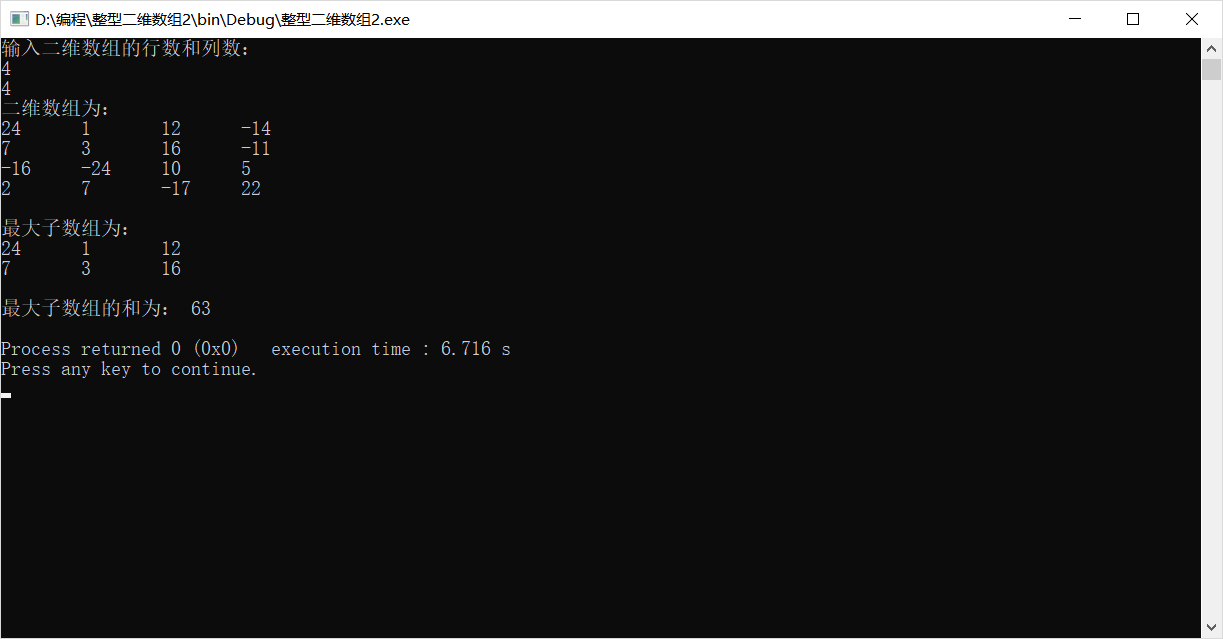
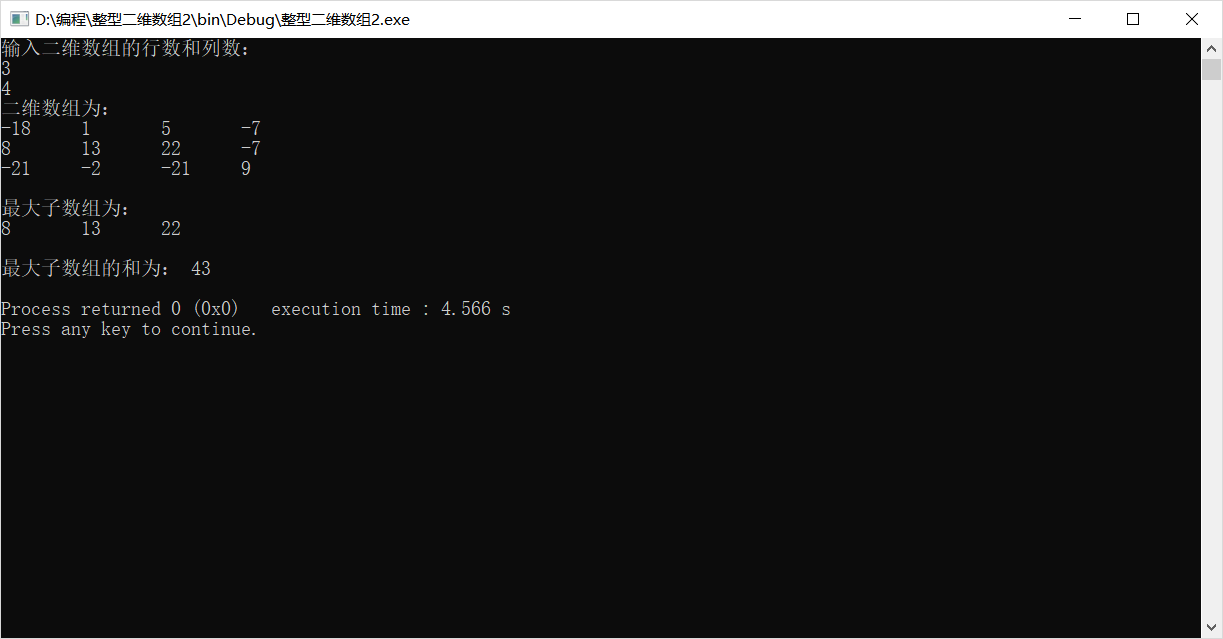
遇到的问题及解决方法：

日期	编号	类型	引入阶段	排除阶段	修复时间	修复缺陷
10.20	1	循环函数错误	设计阶段	编码	40min	查找资料，完善设计思路
	描述：对如何实现最大子数组的查找思路不明确，查找并借阅相关资料，完善设计思路
10.20	2	函数错误	编码	编译	30min	反复调试，查找资料
	描述：对函数编写不熟悉，bug太多，反复编译并查找错误

体会：

对如何查找二维整数数组最大子数组的和有了深刻的理解，对循环函数的使用也更加熟悉，但是，由于编程能力有限，无法解决算法时间复杂度的问题。上述编程的时间复杂度为O（n^3）,不能达到时间复杂度为O（n）

的目标。

合作图片：

组内成员：张素颖，于芳娜