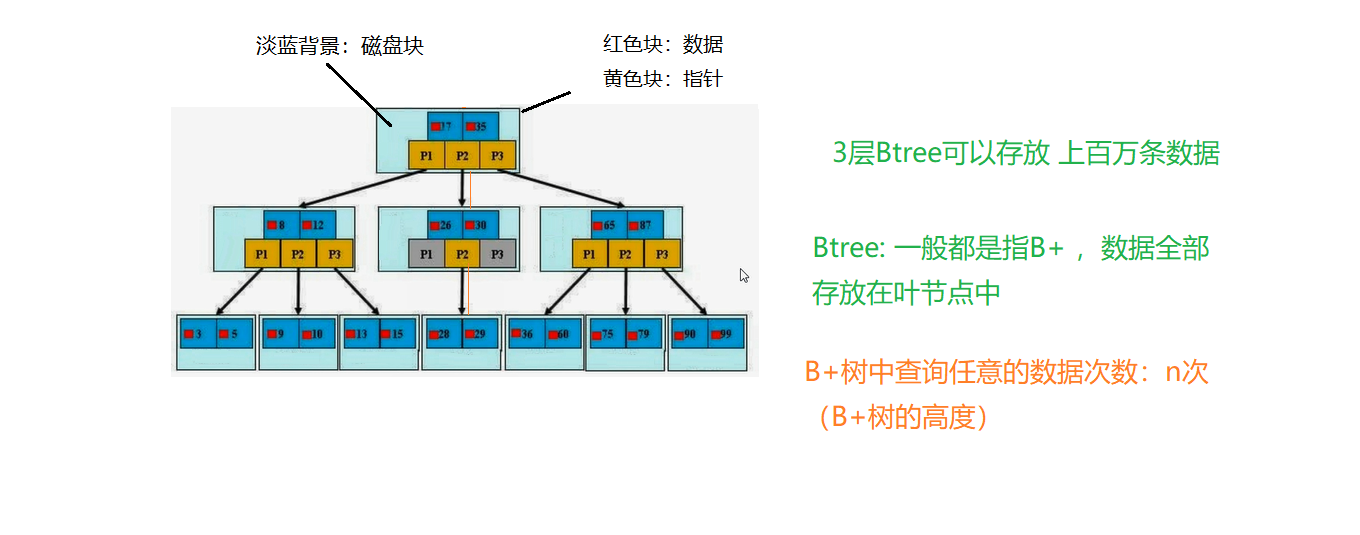
简单概述:
在我们存数据时, 如果建立索引。 数据库系统会维护一个满足特定查找算法的数据结构,这些数据结构以某种方式引用数据
可以在这些数据结构之上,实现高级查找算法,这种结构就是索引
一般来说, 索引本身也很大, 不可能全部存储在内存中, 因此索引往往以索引文件的形式存储在磁盘上
为了加快数据的查找,可以维护二叉查找树, 每个节点分别包含索引键值和一个指向对应数据记录的物理地址的指针,
这样就可以运用二叉查找在一定的复杂度内获取相应的数据,从而快速的检索出符合条件 的记录
除了二叉树还有BTtree索引 我平时所说的索引,如果没有特别指定, 都是指B树结构组织的索引
其中聚焦索引,次要索引,复合索引,前缀索引,唯一默认都是B+树索引 除B+树索引之外, 还有哈希索引(Hash index)等
二叉查找树:
特点:若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点(no duplicate nodes)
图解演示:
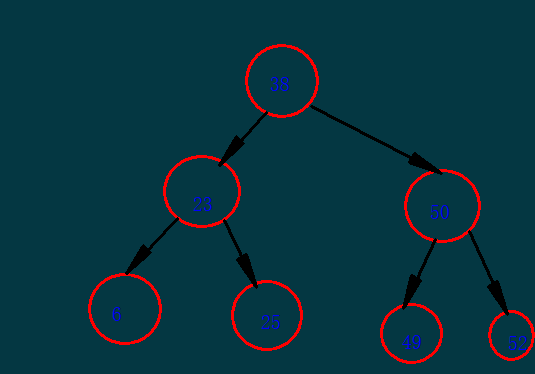
分析:使用这种方法可以快速的帮助我们定位到查找的数据,如果查找数据为52时,我们第一步从根结点37开始,发现比38大,到右边50查找,再发现
比50大,再到右边查找,3次就可以查找到位置。但是这个并不是最好的查找方法,如果我们查找的数据只在一边显示,这个查找速度还是很慢的
B-Tree 平衡多路查找树:
特点:m阶B-Tree满足以下条件:
0.根节点至少包括两个孩子 红色代表关键字
1.树中每个节点最多有m个孩子(m>=2)
2. 除了根节点和叶子节点外,其它每个节点至少有Ceil(m/2)个孩子。
3. 所有叶子节点都在同一层
4. ki(1=1…n)为关键字,且关键字按顺序升序排列k(i-1) < k 8 < 9 (红色的是关键字 左边的数要小于右边)
5. 关键字的个数n满足:ceil(m/2)-1 <= n <= m-1 (非叶子节点关键字个数比指向孩子的指针少1个)
6. 非叶子结点的指针p[1],p[2],…p[m] 其中p1指向关键字小于k[1]的子树 3 < 8
p[m]指针关键字大于k[m-1]的子树 15 > 12
p[i]指向关键字属于(k[i-1],k[i])的子树 9,10 是位于8 和 12之间
图示: