题目:https://leetcode-cn.com/problems/permutations/
给定一个没有重复数字的序列,返回其所有可能的全排列。
样例输入与输出:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
思路:
- 标准的全排列问题,用dfs的方法实现,
vis[]记录元素是否已经访问过,以避免在递归中重复取到元素,可以算做dfs的一个模板,不难得出解答树:
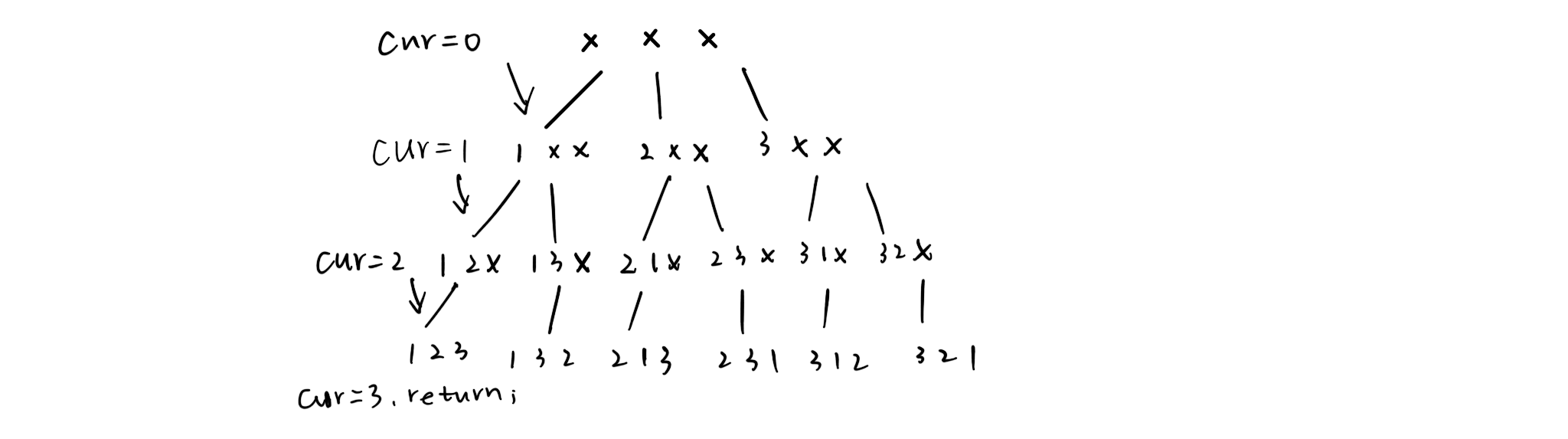
代码:
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
tmp.resize(nums.size());
vis.resize(nums.size());
dfs(nums, 0, ans);
return ans;
}
private:
vector<int> tmp;
vector<int> vis;
void dfs(vector<int>& nums, int cur, vector<vector<int> >& ans){
if(cur == nums.size()){
ans.push_back(tmp);
return;
}
for(int i = 0; i < nums.size(); ++i){
if(!vis[i]){
vis[i] = 1;
tmp[cur] = nums[i];
dfs(nums, cur+1, ans);
vis[i] = 0;
}
}
}
};
- 官方题解上有一个更快的做法,不需要借助
vis[]和tmp[]数组,将在tmp[]数组中放入元素的操作用swap()替换,思路是一样的,只是这样做效率更高。
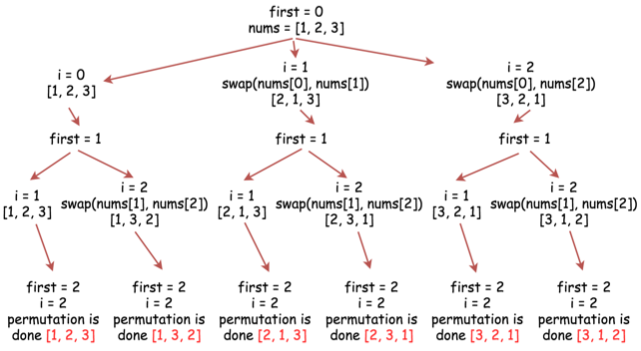
代码:
class Solution {
public:
void dfs(int cur, int n, vector<int>& nums, vector<vector<int>>& ans){
if(cur == n){
ans.push_back(nums);
}
for(int i = cur; i < n; ++i){
swap(nums[i], nums[cur]);
dfs(cur+1, n, nums, ans);
swap(nums[i], nums[cur]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
dfs(0, nums.size(), nums, ans);
return ans;
}
};