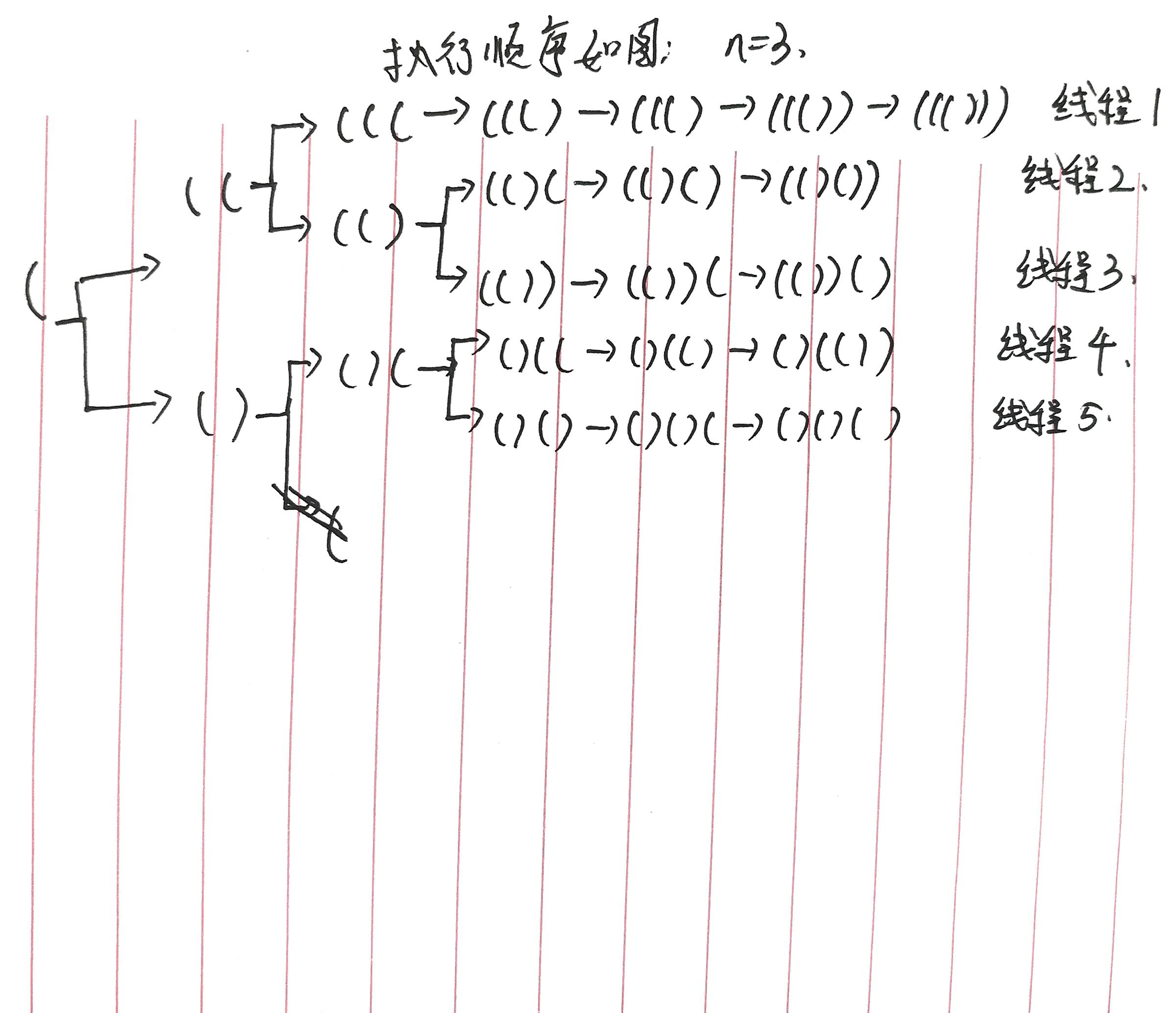leetcode-生成括号（回溯算法）

 转载出处：https://blog.csdn.net/yanerhao/article/details/68561290

生成括号

 

 

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

从题目寻找三要素：

1 选择：

加左括号

加右括号

2 条件

左括号没有用完（才可以加左括号）

右括号数目小于左括号数目（才可以加右括号）

3 结束

左右括号均用完

思路：

if (左右括号都已用完) {
  加入解集，返回
}
//否则开始试各种选择
if (还有左括号可以用) {
  加一个左括号，继续递归
}
if (右括号小于左括号) {
  加一个右括号，继续递归
}

代码如下：

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> list=new ArrayList();
        backTrace(n,n,"",list);
        return list;
    }
    void backTrace(int left,int right,String out,List<String> list){
        if(left==0&&right==0){
            list.add(out);
            return;
        }
        if(left>0){
            backTrace(left-1,right,out+"(",list);
        }
        if(right>left){
            backTrace(left,right-1,out+")",list);
        }
    }
}

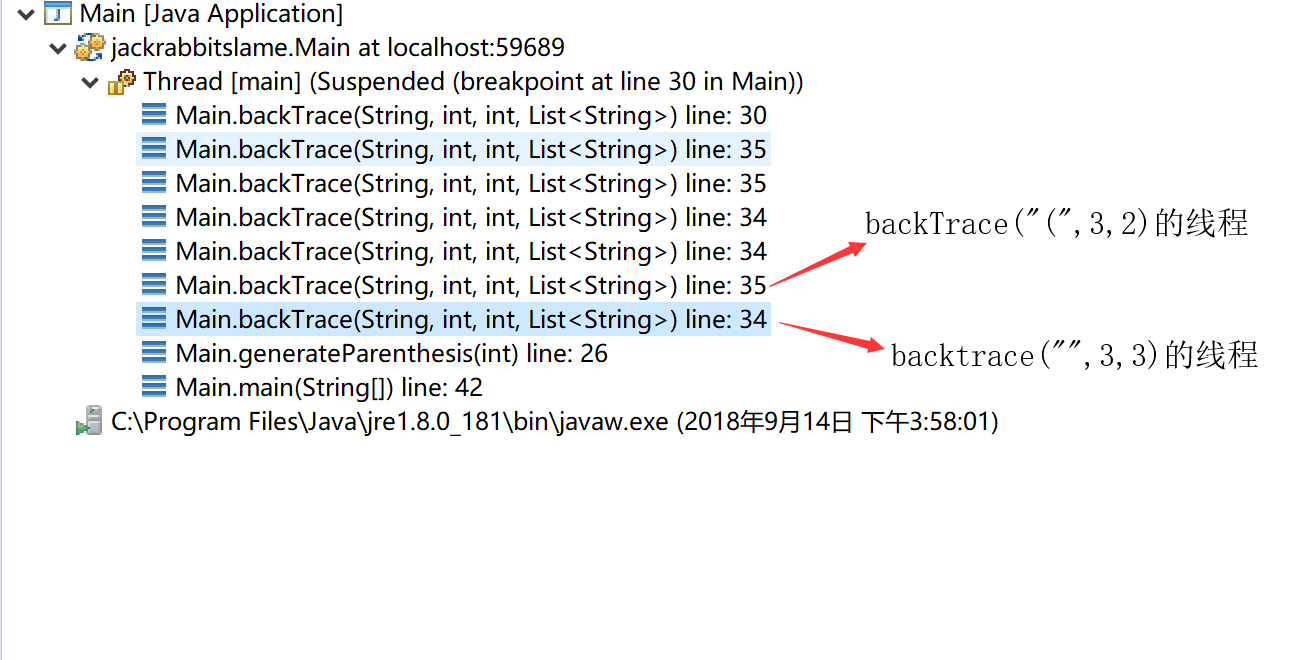
 总结：在做第二遍的时候发现，如何解决这个分支的问题，根据判定条件，你需要添加左括号和右括号。发现，回溯的算法是计算到他的边界位置，这里用两个if()的条件，可以顺利的分支为添加左括号和右括号。下面是通过Debug展示的回溯算法在计算过程中的真实操作。 在进行  generateParenthesis(int n) 方法时，其实生成了许多条线程来向下探索。

通过这里，其实体现了递归和回溯的类似。两者在分支的情况下，都是生成了2个线程，不断递归，就是不断生成新的线程。