LeetCode430 扁平化多级双向链表

您将获得一个双向链表，除了下一个和前一个指针之外，它还有一个子指针，可能指向单独的双向链表。这些子列表可能有一个或多个自己的子项，依此类推，生成多级数据结构，如下面的示例所示。

扁平化列表，使所有结点出现在单级双链表中。您将获得列表第一级的头部。

 

示例:

输入:
 1---2---3---4---5---6--NULL
         |
         7---8---9---10--NULL
             |
             11--12--NULL

输出:
1-2-3-7-8-11-12-9-10-4-5-6-NULL

 

以上示例的说明:

给出以下多级双向链表:

 

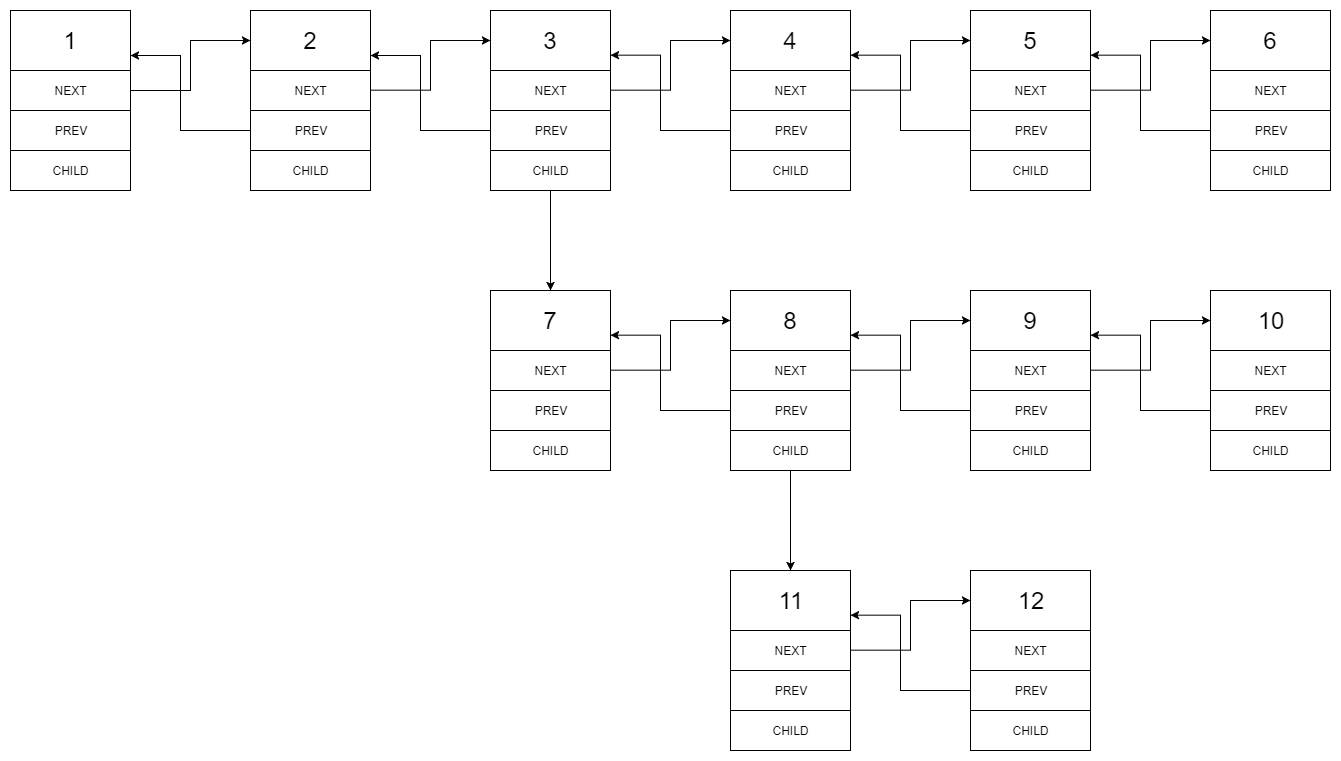
我们应该返回如下所示的扁平双向链表:

---

//章节 - 链表    
//四、小结
//3.扁平化多级双向链表
/*
算法思想：
    题意较复杂，先读懂题意，可以看出如果某个结点有下一层双向链表，那么下一层双向链表中的结点就要先加入进去，如果下一层链表中某个结点还有下一层，那么还是优先加入下一层的结点，整个加入的机制是DFS的，就是有岔路先走岔路，走到没路了后再返回，这就是深度优先遍历的机制。
    采用迭代，迭代的写法与递归是反过来的，先把第二层加入第一层，此时第二层底下可能还有很多层，不必理会，之后等遍历到的时候，再一层一层的加入第一层中，最终都可以压平。
*/
//算法实现：
/*
// Definition for a Node.
class Node {
public:
    int val = NULL;
    Node* prev = NULL;
    Node* next = NULL;
    Node* child = NULL;

    Node() {}

    Node(int _val, Node* _prev, Node* _next, Node* _child) {
        val = _val;
        prev = _prev;
        next = _next;
        child = _child;
    }
};
*/
class Solution {
public:
    Node* flatten(Node* head) {
        Node *cur = head;
        while (cur) {
            if (cur->child) {   //如果有孩子，既有下一层
                Node *next = cur->next;     //保存断开点
                Node *last = cur->child;    //进入下一层
                while (last->next) 
                    last = last->next;
                cur->next = cur->child;
                cur->next->prev = cur;
                cur->child = NULL;
                last->next = next;
                if (next) 
                    next->prev = last;    
            }
            cur = cur->next;
        }
        return head;
    }
};